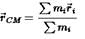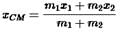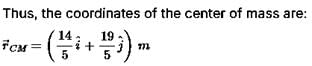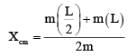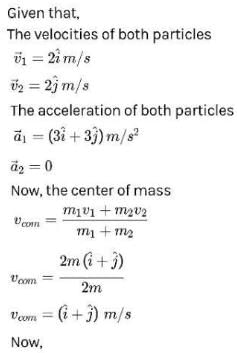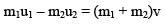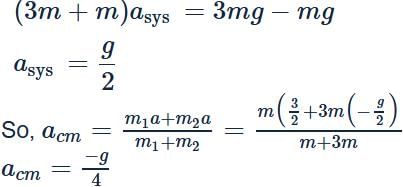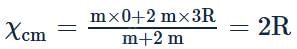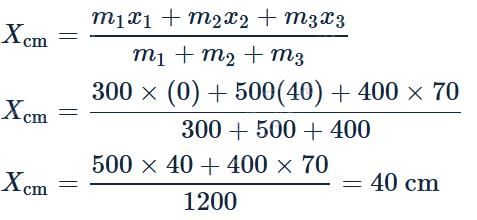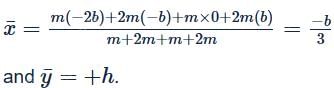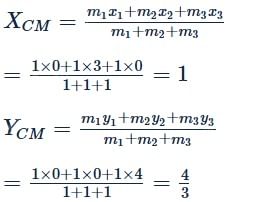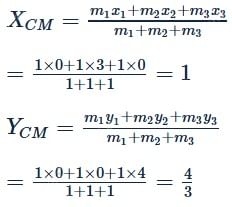Test: Centre Of Mass (Competition Level) - JEE MCQ
30 Questions MCQ Test - Test: Centre Of Mass (Competition Level)
A square plate and a circular plate made up of same material are placed touching each other on a horizontal table. If the side length of square plate is equal to diameter of the circular plate, then the centre of mass of the combination will be
A rigid body consists of a 3 kg mass located at  and a 2 kg mass located at
and a 2 kg mass located at 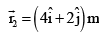 .The position of center of mass is
.The position of center of mass is
A dog weighing 5 kg is standing on a flat boat so that it is 10 meters from the shore. It walks 4 m on the boat towards the shore and then halts. The boat weighs 20 kg and one can assume that there is no friction between it and water. The dog from the shore at the end of this time is
Particles of masses 1 kg and 3 kg are at m then instantaneous position of their centre of mass is
A uniform metre rod is bent into L shape with the bent arms at 90o to each other. The distance of the centre of mass from the bent point is
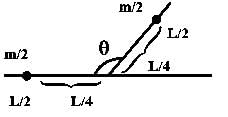
A thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
Two identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
Two particles of equal masses have velocities First particle has an acceleration
while the acceleration of the other particle is zero. The centre of mass of the two particles moves in a path of
Two bodies of masses m1 and m2 are moving with velocity v1 and v2 respectively in the same direction. The total momentum of the system in the frame of reference attached the centre of mass is (v is relative velocity between the masses)
A body of mass m moving at a constant velocity v hits another body of the same mass moving with a velocity v/2 but in the opposite direction and sticks to it. The common velocity after collision is
A body of mass 5 kg is acted on by a net force F which varies with time t as shown in graph, then the net momentum in SI units gained by the body at the end of 10 seconds is
A force time graph for the motion of a body is as shown in figure. Change in linear momentum between 0 and 6 s is
A ball of mass 10 g hits a hard surface vertically with a speed of 5 m/s and rebounds with the same speed. The ball remains in contact with the surface for 0.01 s. The average force exerted by the surface on the ball is
Locate the centre of mass of a uniform semicircular ring (or wire) of radius R and linear mass density λ.
The linear momentum of a particle varies with time t as p = a + bt + ct2. Which of the following statement is correct?
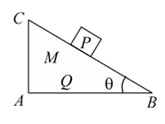
A block Q of mass M is placed on a horizontal frictionless surface AB and a body P of mass m is released on its frictionless slope. As P slides by a length L on this slope of inclination θ, the block Q would slide by a distance
A bomb of mass 12 kg, initially at rest explodes into two pieces of masses 4 kg and 8 kg. The speed of the 8 kg mass is 6 m/s. The kinetic energy of the 4 kg mass is
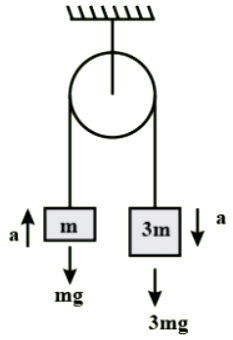
A pulley fixed to the ceiling carries a string with blocks of mass m and 3 m attached to its ends. The masses of string and pulley are negligible. When the system is released, its centre of mass moves with what acceleration?
A 1 kg ball moving at 12 m/s collides head-on with a 2 kg ball moving in the opposite direction at 24 m/s. If the coefficient of restitution is 2/3 then the final speeds of the two balls are respectively
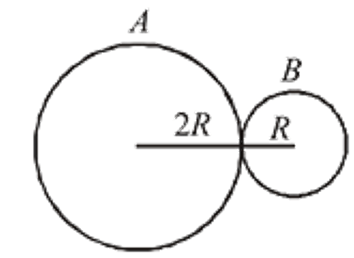
Two spheres A and B of masses m and 2m and radii 2R and R respectively are placed in contact as shown. The COM of the system lies
Ball 1 collides with another identical ball 2 at rest as shown in figure. For what value of coefficient of restitution e, the velocity of second ball becomes two times that of 1 after collision
There are some passengers inside a stationary railway compartment. The centre of mass of the compartment itself (without the passengers) is C1, while the centre of mass of the 'compartment plus passengers' system is C2. If the passengers move about inside the compartment then
“A truck of mass 15 tons moving with one meter per second collides with the stationary truck of 10 tons and they start to move together.
In the above question, the energy lost in the collision is”
Three masses are placed on the x -axis :300 g at origin, 500 g at x=40 cm and 400 g at x=70 cm. The distance of the centre of mass from the origin is
A particle of mass 1 g moving with a velocity m/s experiences a perfectly inelastic collision with another particle of mass 2 g and moving with velocity
m/s. The velocity of the combined particle is
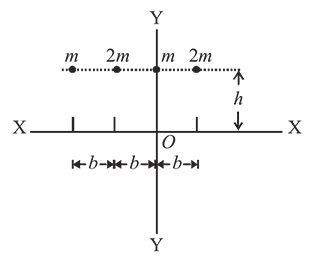
With O as the origin of the coordinate axis, the X and Y-coordinates of the centre of mass of the system of particles shown in the figure may be given as? (Here m and 2m represent the masses of the particles)
A batsman deflects a ball at an angle 90o without changing its initial speed which is equal to 54 km/h. The impulse imparted to the ball whose mass is 0.5 kg is
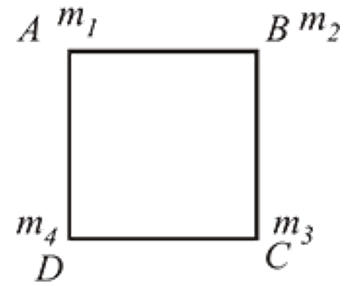
Four particles of masses m1, m2, m3 and m4 are placed at the vertices A,B C and D as respectively of a square shown. The COM of the system will lie at diagonal AC if
A ball moving with a constant speed hits another identical ball at rest. If co-efficient of restitution equals (2/3) then the ratio of speeds of the second ball to that of the first ball after collision will be
The centre of mass of three bodies each of mass 1 kg located at the points (0,0),(3,0) and (0,4) in the XY plane is