CUET PG Computer Science Mock Test - 2 - CUET PG MCQ
30 Questions MCQ Test - CUET PG Computer Science Mock Test - 2
In how many ways can the letters of the word 'HEALING' be arranged so that the vowels always come together?
What is the maximum value of sin x ⋅ cos x ?
Select the option that is related to the third word in the same way as the second word is related to the first word.
(The words must be considered as meaningful English words and must not be related to each other based on the number of letters/number of consonants/vowels in the word)
Botany : Plants : : Conchology : ?
Consider the following in respect of matrices A and B of same order:
1) A2 – B2 = (A + B) (A – B)
2) (A – I) (I + A) = O ⇔ A2 = I
Where I is the identity matrix and O is the null matrix.
Which of the above is/are correct?
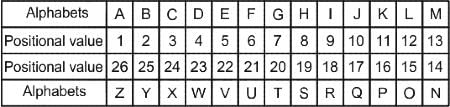
In a certain code language, 'VOCAL' is coded as '90327', 'WAVES' is coded as '31758', 'VOTED' is coded as '42631'. What is the code for 'E' in that code language?
Which of the following alphanumeric clusters will replace the question mark (?) in the series to make it logically complete?
ACE 9, BDF 12, GIK 27, HJL 30, ?, NPR 48, SUW 63
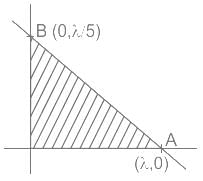
If a line is perpendicular to the line 5x – y = 0 and forms a triangle of area 5 square units with co-ordinate axes, then its equation is
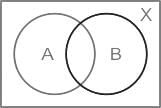
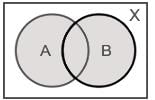
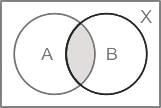
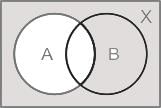
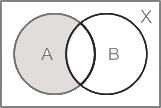
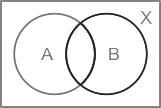
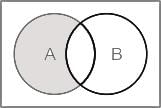
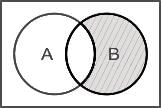
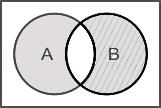
Let A and B be subsets of X and C = (A ∩ B’) ∪ (A’ ∩ B), where A’ and B’ are complements of A and B respectively in X. what is C equal to?
For the next two (2) items that follow:
The integral 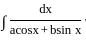 is of the form
is of the form 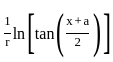
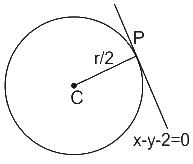
What is r equal to?
Box A contains 2 white and 3 red balls and box B contains 4 white and 5 red balls. One ball is drawn at random from one of the boxes and is found to be red. Then, the probability that it was from box B, is
A straight line x = y + 2 touches the circle 4(x2 + y2) = r2. The value of r is
If a, b, c are in AP or GP or HP, then 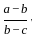 is equal to
is equal to
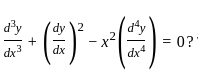
Three statements are given, followed by three conclusions numbered I, II and III. Assuming the statements to be true, even if they seem to be at variance with commonly known facts, decide which of the conclusions logically follow(s) from the statements.
Statements:
Some fathers are females.
All fathers are males.
Some fathers are mothers.
Conclusions:
I. Some males are not females.
II. Some mothers are females.
III. Some males are mothers.
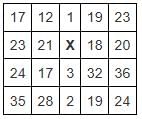
Every element in the central column of the matrix has a simple arithmetic relationship with the pairs on the left and right in the corresponding row.

What would be the value of X?
Given below is a question followed by two statements. Analyze and decide whether the question can be answered from the given statements.
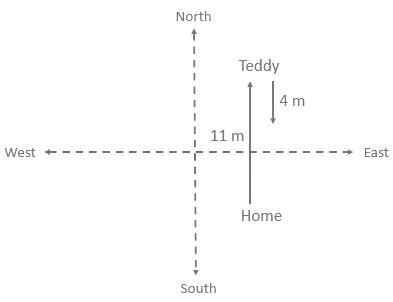
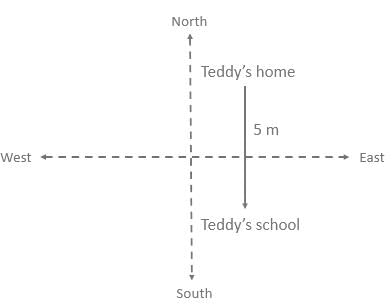
Question: How far is Teddy from his home?
Statement I: Teddy started walking towards the north direction from his home till 11 meters and returned back in the same direction and stopped at the stop after walking for 4 meters.
Statement II: Teddy took a left turn from his school and walked for 5 meters.
Let X be a non-empty set and let A, B, C be subsets of X, consider the following statements:
1) A ⊂ C ⇒ (A ∩ B) ⊂ (C ∩ B), (A ∪ B) ⊂ (C ∪ B)
2) (A ∩ B) ⊂ (C ∩ B) for all sets B ⇒ A ⊂ C
3) (A ∪ B) ⊂ (C ∪ B) for all sets B ⇒ A ⊂ C
Which of the above statements is/are correct?Consider the following statements:
1. f(x) = [x], where [.] is the greatest integer function, is discontinuous at x = n, where n ϵ Z.
2. f(x) = cot x is discontinuous at x = nπ, where n ϵ Z.
Which of the above statements is/are correct?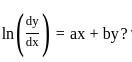
Consider the following statements:
1. Derivative of f(x) may not exist at some point.
2. Derivative of f(x) may exist finitely at some point.
3. Derivative of f(x) may be infinite (geometrically) at some point.
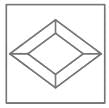
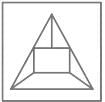
Which of the above statements are correct?From the following figures choose that figure which is different from the other:
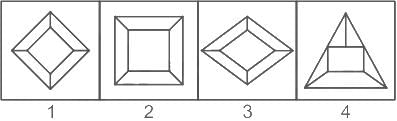


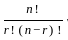

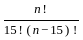 ------(3)
------(3)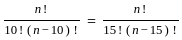
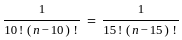
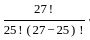 =
= 
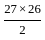 =
= 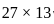 = 351
= 351
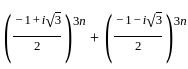 ?
?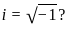
 and ω2 =
and ω2 = 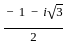
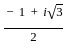 and ω2 =
and ω2 = 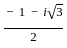
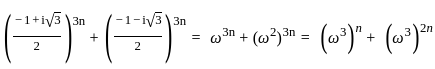 = 1 + 1 = 2
= 1 + 1 = 2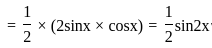
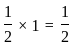
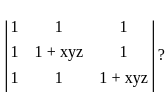
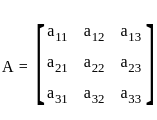 then determinant of A is given by:
then determinant of A is given by: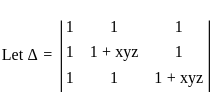
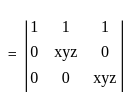
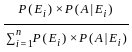 , i = 1, 2, ... n
, i = 1, 2, ... n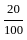 =
= 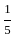
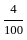 =
= 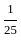
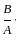 ) =
) =  =
= 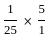


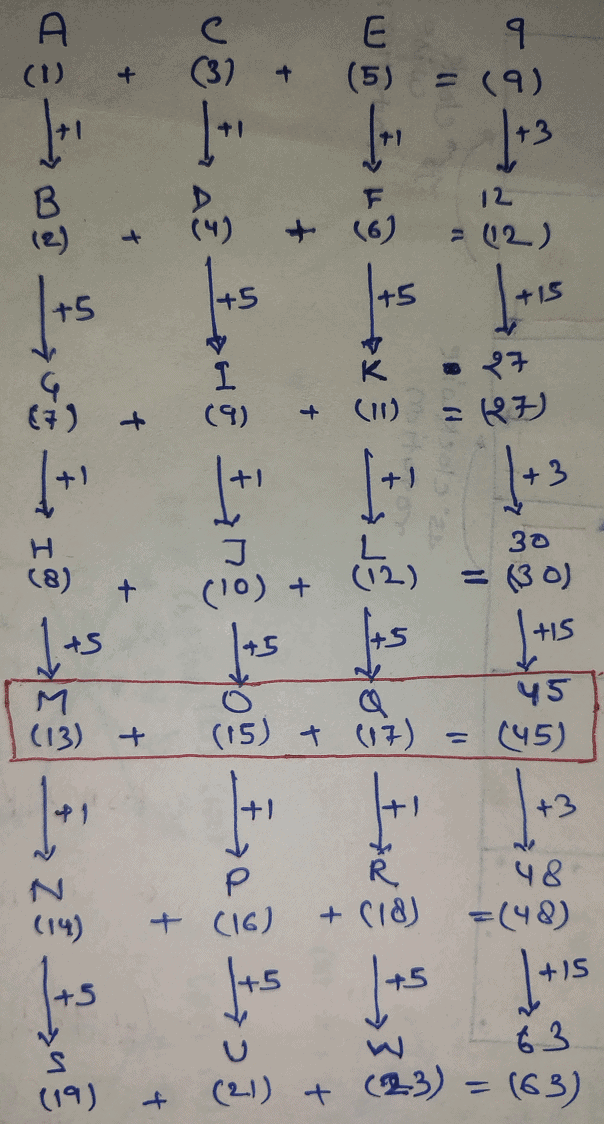
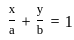 , Where a is the x- intercept and b is the y- intercept.
, Where a is the x- intercept and b is the y- intercept.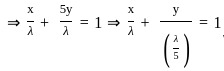
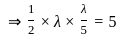


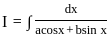
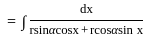
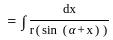
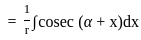
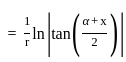
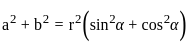
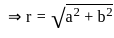
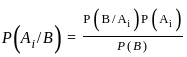


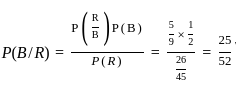
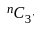
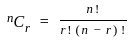
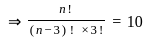

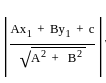
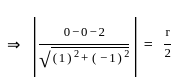

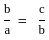
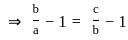
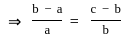
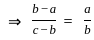
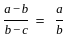
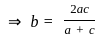

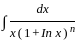 equal to (n ≠ 1) ?
equal to (n ≠ 1) ?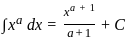
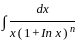
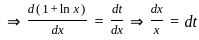 -----(1)
-----(1)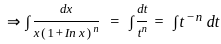
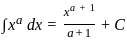
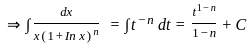
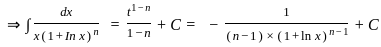


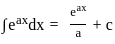
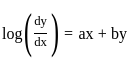
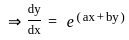
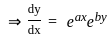
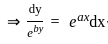
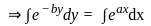
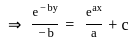
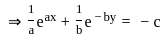
 (∵ -c = c)
(∵ -c = c)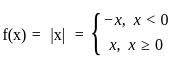
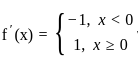
 → Here, a quadrilateral is present inside and outside.
→ Here, a quadrilateral is present inside and outside.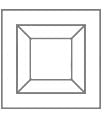
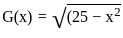 then what is
then what is 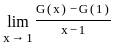 equal to?
equal to?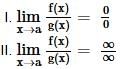
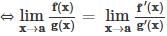
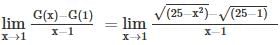
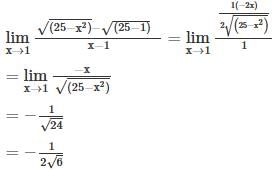
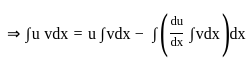
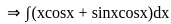 (∵ elog x = x)
(∵ elog x = x)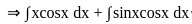
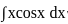
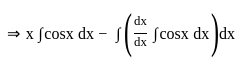
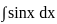 + c
+ c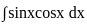
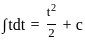
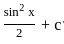
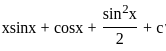 .
.















