1) Identify the Feasible Region
The feasible region is given by the intersection of all these half-planes (plus nonnegativity constraints). We typically look at corner points to find the maximum or minimum in a linear program.
2) Find Corner Points
a) Intersection with x₁ = 0
- From (1): 3(0) + 5x₂ ≤ 15 ⟹ x₂ ≤ 3.
- From (2): 5(0) + 2x₂ ≤ 10 ⟹ x₂ ≤ 5.
The tighter bound is x₂ ≤ 3.
So one corner is (0, 3).
b) Intersection with x₂ = 0
- From (1): 3x₁ + 5(0) ≤ 15 ⟹ x₁ ≤ 5.
- From (2): 5x₁ + 2(0) ≤ 10 ⟹ x₁ ≤ 2.
The tighter bound is x₁ ≤ 2.
So another corner is (2, 0).
c) Intersection of the two lines
{3x1+5x2=155x1+2x2=10{3x1+5x2=155x1+2x2=10Solve systematically:
-
From the first equation:
3x₁ = 15 − 5x₂ ⟹ x₁ = (15 − 5x₂)/3. -
Substitute into the second equation:
5\bigl(\tfrac{15 − 5x₂}{3}\bigr) + 2x₂ = 10
⇒ (75 − 25x₂)/3 + 2x₂ = 10
⇒ 75 − 25x₂ + 6x₂ = 30 (after multiplying both sides by 3)
⇒ 75 − 19x₂ = 30
⇒ −19x₂ = −45
⇒ x₂ = 45/19. -
Then x₁ = (15 − 5·(45/19))/3 = (15 − 225/19)/3 = (285/19 − 225/19)/3 = (60/19)/3 = 20/19.
Hence the intersection point is (20/19, 45/19).
d) Also check (0,0)
- That obviously satisfies 3(0) + 5(0) ≤ 15 and 5(0) + 2(0) ≤ 10, so (0,0) is in the feasible region.
So the corner points are (0,0), (0,3), (2,0), and (20/19, 45/19).
3) Evaluate the Objective Function at Each Corner
The objective function is
z = 2.5x₁ + x₂.
-
At (0,0):
z = 2.5(0) + 0 = 0. -
At (0,3):
z = 2.5(0) + 3 = 3. -
At (2,0):
z = 2.5(2) + 0 = 5. -
At (20/19, 45/19):
z = 2.5 × (20/19) + (45/19).- 2.5 × (20/19) = 50/19,
- so total = (50/19) + (45/19) = 95/19 = 5.
Thus, the maximum objective value is 5, attained at both (2,0) and (20/19, 45/19).
4) Check for Multiple Optimal Solutions
Since the same maximum value z = 5 occurs at two distinct corner points, it typically indicates that every point on the line segment between those two points will also yield z = 5. Indeed, if you pick any point on the line segment connecting (2,0) and (20/19, 45/19), you get the same objective value 5.
Therefore, the maximum value of z is unique (that is, 5), but there are infinitely many solutions (an entire line segment in the feasible region) that achieve this maximum.
Conclusion
The correct characterization is:
Unique value of Maxz with infinite number of feasible solutions.
Hence, among the provided choices, that corresponds to:
(a) Unique value of Maxz with infinite number of feasible solution.


 is solenoidal then values of 'a' is
is solenoidal then values of 'a' is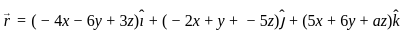
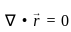 where
where 
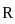 has a limit point.
has a limit point.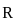 , a sequence is convergent if and only if it is Cauchy.
, a sequence is convergent if and only if it is Cauchy.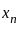 ⟩=⟨−1,1,−1,1,−1,1,…⟩ is an example of a bounded sequence that oscillates finitely.
⟩=⟨−1,1,−1,1,−1,1,…⟩ is an example of a bounded sequence that oscillates finitely.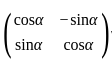 and A + A' = I, then the value of
and A + A' = I, then the value of 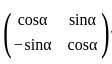 where,
where, 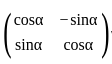
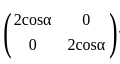 =
= 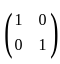
 has
has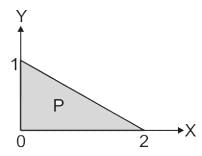
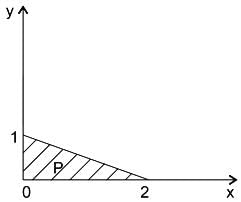
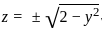
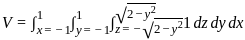
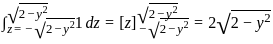
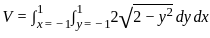

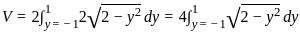
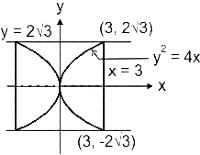
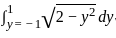 represents the area of a semicircle with radius
represents the area of a semicircle with radius 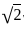
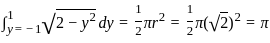
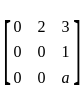 Here 0 and a are the eigenvalues and eigenspace of A for 0 is 1
Here 0 and a are the eigenvalues and eigenspace of A for 0 is 1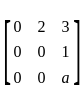 ,
, 
 ,
,

 where
where 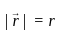 and
and 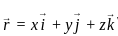 will be
will be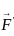 Irrotational if
Irrotational if 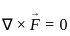
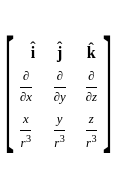
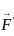 is solenoidal
is solenoidal 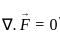
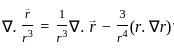
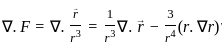
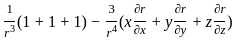
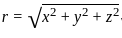
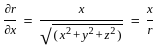
 ,
, 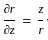
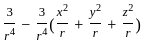
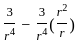
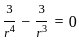
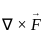 =
= 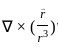 =
= 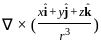
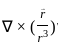 =
= 

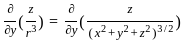
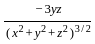
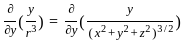 =
=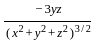
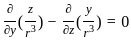
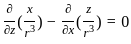 &
& 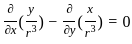
 =0
=0