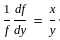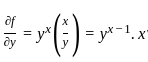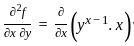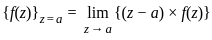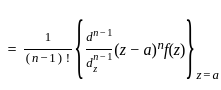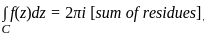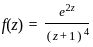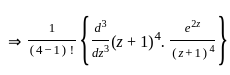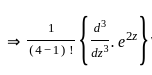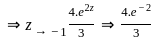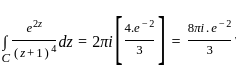CUET PG Mathematics Mock Test - 4 - CUET PG MCQ
30 Questions MCQ Test - CUET PG Mathematics Mock Test - 4
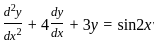
The particular integral for the differential equation is:
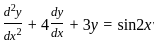
The particular integral for the differential equation is:
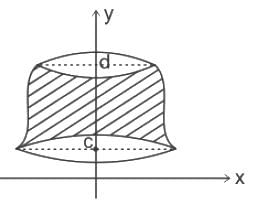
The volume generated by revolving the arc 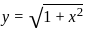 lying between x = 0 and x = 4 about x - axis is
lying between x = 0 and x = 4 about x - axis is
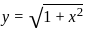 lying between x = 0 and x = 4 about x - axis is
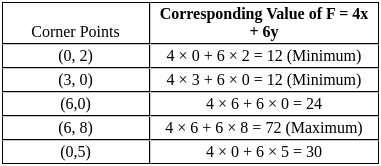
lying between x = 0 and x = 4 about x - axis isCorner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8), and (0, 5).
Let F = 4x + 6y be the objective function.
Maximum of F – Minimum of F =
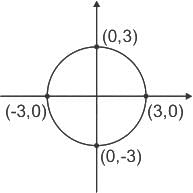
If C is the circle x2 + y2 = 1 taken in anti-clockwise direction then
∫c[(x2015 y2016 + 2014y) dx + (x2016 y2015 + 2017x) dy] will be
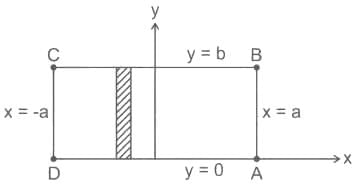
Evaluate  for
for 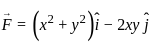 taken around the rectangle bounded by the lines x = ± a, y = 0, y = b.
taken around the rectangle bounded by the lines x = ± a, y = 0, y = b.
Let (an) be a sequence of real numbers defined by
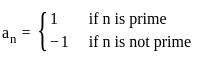
Let bn = an/n for n ∈ ℕ. Then
Let F be the family of curves given by
x2 + 2hxy + y2 = 1, − 1 < h < 1 .
Then, the differential equation for the family of orthogonal trajectories to F is
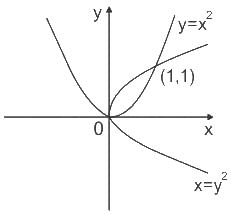
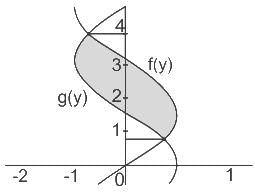
f(x, y) is a continuous function defined over (x, y) ∈ [0, 1] × [0, 1]. Given the two constraints, x > y2 and y > x2, the area under f(x, y) is
Let f(z) = exp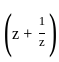 , z ∈ ℂ\{0}. The residue of f at z = 0 is
, z ∈ ℂ\{0}. The residue of f at z = 0 is
If a function f(z) is continuous at Z = Z0, then which of the following statements does not hold?
Let H be a subgroup of the group G and 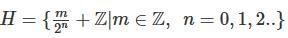 then choose the correct option?
then choose the correct option?
Let G be a finite group and H is a subgroup of G then Which of the following statements must be true?
The expansion of power series having R as the radius of convergence and x, a be any two points in R, converges if ______.
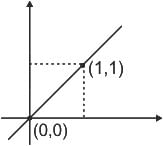
The value (up to two decimal places) of a line integral:
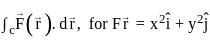
along C which is a straight line joining (0, 0) to (1, 1) is ______
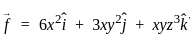 at the point (2, 3, 4).
at the point (2, 3, 4).
Value of the integral∬(x2 + y2) dx dy over the area bounded by the curves y = x2 and y2 = x is
If 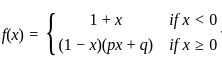
What is the value of 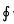
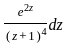 , where c is a circle at origin |z| =3?
, where c is a circle at origin |z| =3?



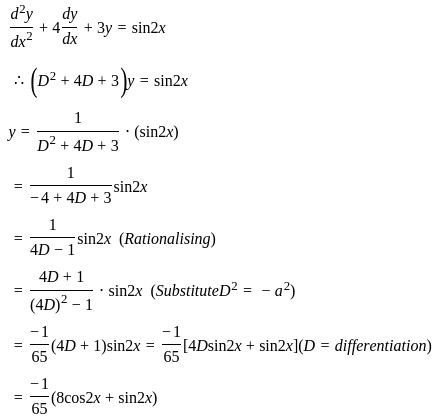
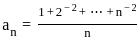 for n ∈ ℕ. Then
for n ∈ ℕ. Then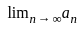 = l then
= l then 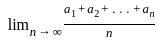 = l
= l is convergent if p > 1 and divergent if p ≤ 1
is convergent if p > 1 and divergent if p ≤ 1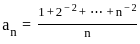
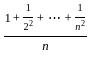
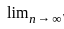
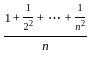 =
= 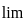
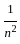 = 0
= 0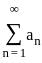 =
= 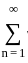
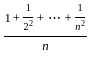
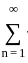
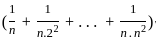
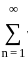
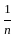 <
< 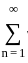

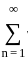
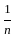 is divergent by p-series test
is divergent by p-series test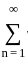
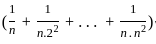 is divergent.
is divergent.
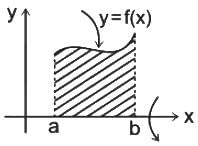
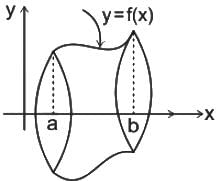
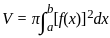
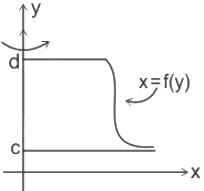
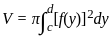
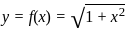 and a = 0, b =
and a = 0, b =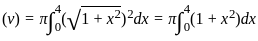
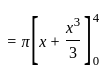
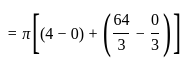
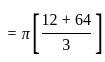
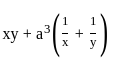 is
is for the given function
for the given function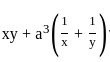
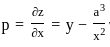 and
and 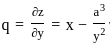
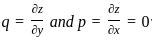 and solving two equations we get
and solving two equations we get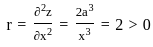 ,
, 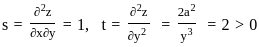
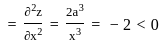 ,
, 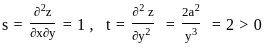
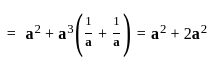 = 3a2.
= 3a2.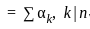 and αk is the number of elements of order k in G'
and αk is the number of elements of order k in G'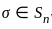 has the cycle decomposition {n
has the cycle decomposition {n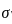
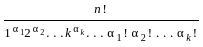 .
.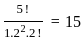
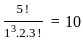
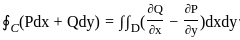
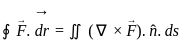
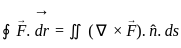
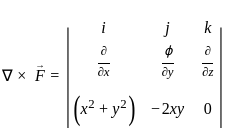
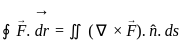
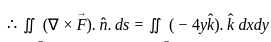
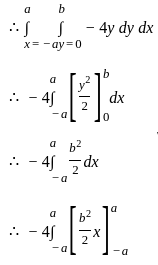
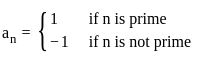
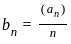 =
= 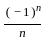 which is bounded lies between - 1 to 1
which is bounded lies between - 1 to 1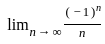 = 0
= 0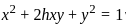 , − 1 < h < 1 .
, − 1 < h < 1 .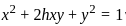
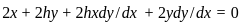
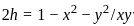
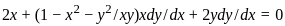
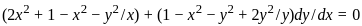
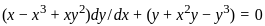
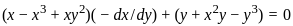
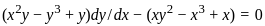
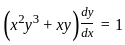 is
is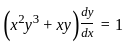

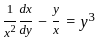
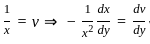
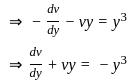
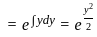
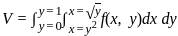
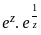
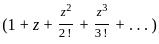
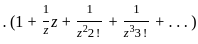
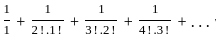
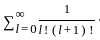
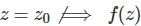
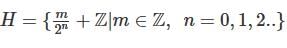
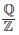
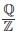
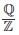
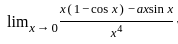 exist and finite then the value of a is
exist and finite then the value of a is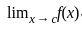 =
= 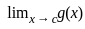 = 0 or ± ∞ and g'(x) ≠ 0 for all x in I with x ≠ c and
= 0 or ± ∞ and g'(x) ≠ 0 for all x in I with x ≠ c and 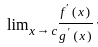 exist then
exist then 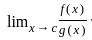 =
= 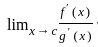
 (0/0 form so using L'hospital rule)
(0/0 form so using L'hospital rule)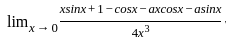
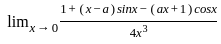
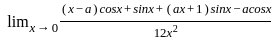

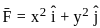
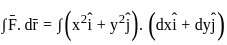
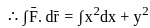
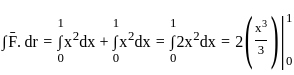
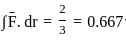
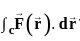
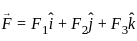
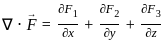
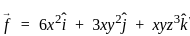
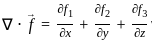 -----(1)
-----(1)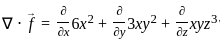
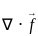 = 12x + 6xy + 3xyz2
= 12x + 6xy + 3xyz2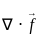 = 12(2) + 6(2)(3) + 3(2)(3)(4)2
= 12(2) + 6(2)(3) + 3(2)(3)(4)2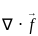 = 24 + 36 + 288 = 348
= 24 + 36 + 288 = 348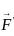 taken over a closed surface ‘S’ is equal to the
taken over a closed surface ‘S’ is equal to the 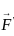 taken over a volume enclosed by the closed surface ‘S’.
taken over a volume enclosed by the closed surface ‘S’.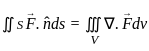
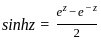
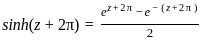
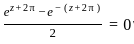
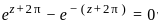
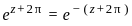
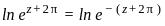
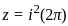
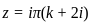 where k = 0i, 1i............ni
where k = 0i, 1i............ni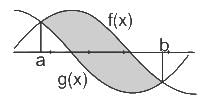
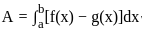
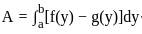

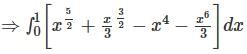
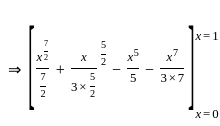
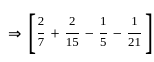
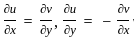 and if it possesses all the partial derivatives then the function f(z) is analytic.
and if it possesses all the partial derivatives then the function f(z) is analytic.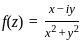

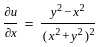
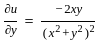 ,
, 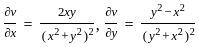
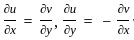 is satisfied and all the partial derivatives are exist except origin(0,0)
is satisfied and all the partial derivatives are exist except origin(0,0)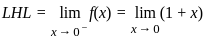
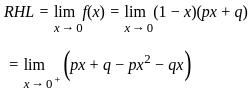
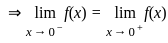
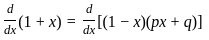
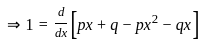
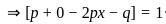
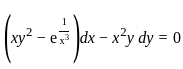 is
is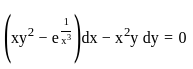
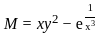
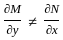

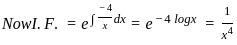
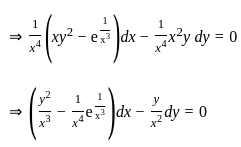
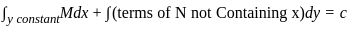
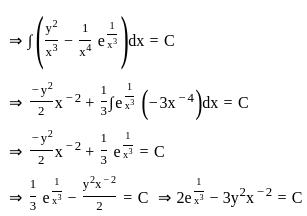
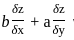 equals to
equals to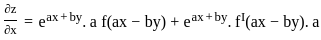
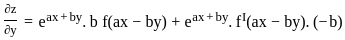
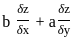
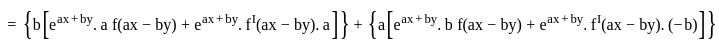
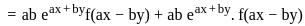
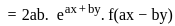
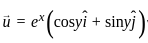 is
is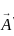 is defined as:
is defined as: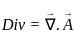
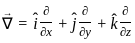
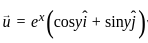
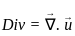
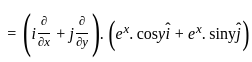
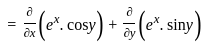
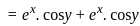
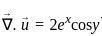
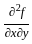 at x = 2, y = 1?
at x = 2, y = 1?