CUET PG Mathematics Mock Test - 5 - CUET PG MCQ
30 Questions MCQ Test - CUET PG Mathematics Mock Test - 5
Which one of the following tests does not give absolute convergence of a series?
Let f be an entire function that satisfies |f(z)| ≤ ey for all z = x + iy ∈ ℂ, where x, y ∈ ℝ. Which of the following statements is true?
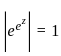 for a complex number z = x + iy, x, y ∈ ℝ, then which of the following is true?
for a complex number z = x + iy, x, y ∈ ℝ, then which of the following is true?
Let {an : n ≥ 1} n be a sequence of real numbers such that 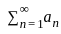 is convergent and
is convergent and 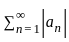 is divergent. Let R be the radius of convergence of the power series
is divergent. Let R be the radius of convergence of the power series 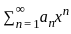 . Then we can conclude that
. Then we can conclude that
 where F(x, y, z) = (y + z, z + x, x + y)
where F(x, y, z) = (y + z, z + x, x + y)
If f(x, y) = xy, then the differential df is equal to
The function f(x) = 8 loge x - x2 + 3 attains its global minimum over the interval [1, e] at x = ________.
(Here loge x is the natural logarithm of x and e2 = 7.39)
Change the order of integration in the following integral
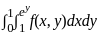 =
= 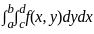
Then find the value of e(a - d) ____
The set of all units in a ring R with unity forms ______.
Find the condition on a, b, c so that the linear system of equations
x + 2y – 3z = a
2x + 6y – 11z = b
x – 2y + 7z = c
is consistentIf 5x + y ≤ 100, x + y ≤ 60, x ≥ 0, y ≥ 0. Then one of the corner points of the feasible region is :
If R is the radius of convergence of any power series then what is the interval of convergence?
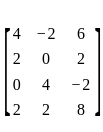
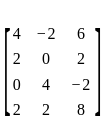
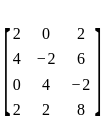
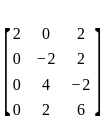
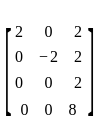
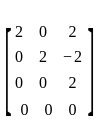
An eigen vector of 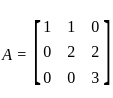 corresponding to minimum eigen value is
corresponding to minimum eigen value is
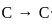 by f(z) = ||z|2 -.1|2. Which of the following statements is true?
by f(z) = ||z|2 -.1|2. Which of the following statements is true?
Find the cardinality of generating set for dihedral group?


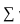
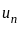 is said to be absolutely convergent if all the terms are positive and the series
is said to be absolutely convergent if all the terms are positive and the series 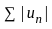 by the modulus of each term of the series is convergent.
by the modulus of each term of the series is convergent.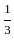 +
+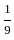 -
-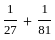 -..... a series ,now if we take the modulus of each term and construct a series then it will look like
-..... a series ,now if we take the modulus of each term and construct a series then it will look like  |=
|=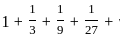 ... ,which is a infinite geometric series with common ratio
... ,which is a infinite geometric series with common ratio 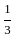 but if we consider the series
but if we consider the series 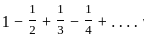 this is a alternating series but if we want to express in sum of absolute term i.e.
this is a alternating series but if we want to express in sum of absolute term i.e.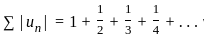
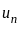
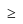
 , (iii)
, (iii)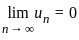 if any alternating series obeys these three conditions then we can say the
if any alternating series obeys these three conditions then we can say the 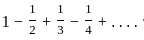
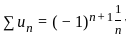
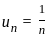
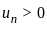

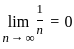
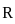 .
.
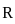 )
)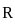 )
)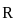 )
)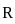 )
)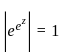 where z = x + iy
where z = x + iy 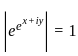
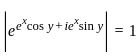
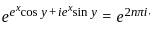
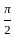
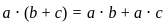 and
and 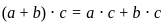 for all a, b, and c in R.
for all a, b, and c in R.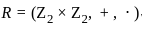 , let's analyze its structure:
, let's analyze its structure: is convergent and
is convergent and  is divergent.
is divergent.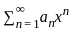 .
.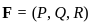 is given by the vector cross product of the del operator with
is given by the vector cross product of the del operator with 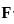 , i.e.,
, i.e., 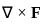 . It is computed as:
. It is computed as: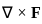 =
= 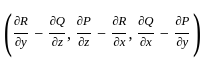
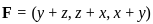 .
.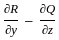 :
: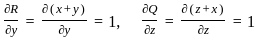
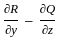 = 1 - 1 = 0
= 1 - 1 = 0 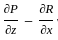 :
: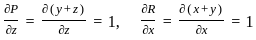
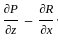 = 1 - 1 = 0
= 1 - 1 = 0 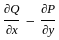 :
: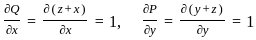
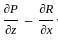
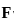 is:
is: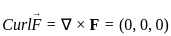
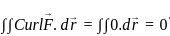
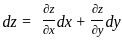
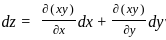
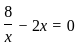
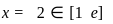

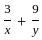 is:
is: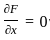
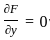
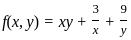
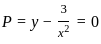 ........(i)
........(i)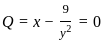 ............(ii)
............(ii)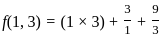
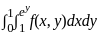
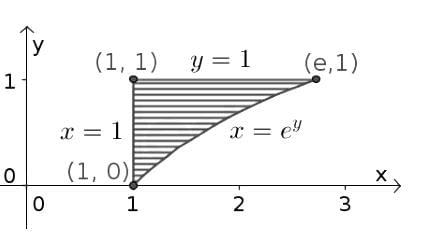
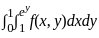
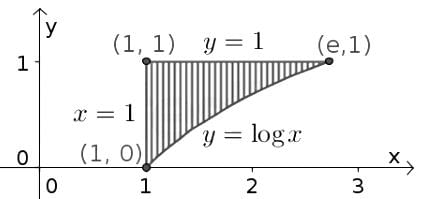
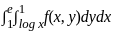
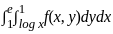 =
= 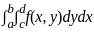
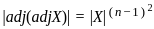
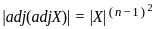
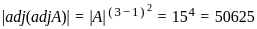
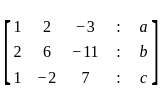
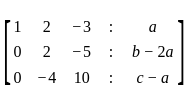
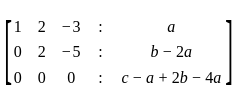
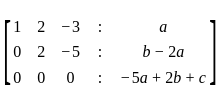
 is a field.
is a field. This quotient ring represents polynomials modulo the ideal generated by
This quotient ring represents polynomials modulo the ideal generated by 

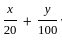 = 1 .....(i)
= 1 .....(i)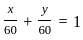 ........(ii)
........(ii)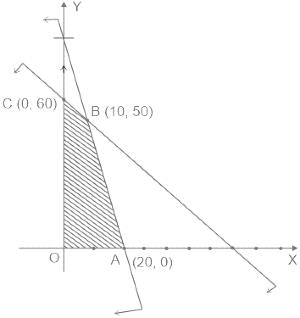
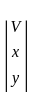 = 0
= 0 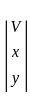 = 0
= 0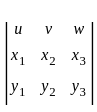 = 0
= 0 is
is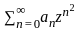
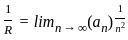
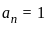
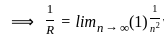
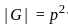
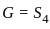 so hence the sum is 15.
so hence the sum is 15.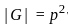 (p is prime) is always abelian.
(p is prime) is always abelian.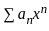 then the series converges when |x| < R i.e., when - R < x < R
then the series converges when |x| < R i.e., when - R < x < R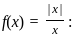
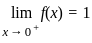
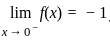
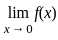 does not exists
does not exists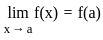 exists or its graph is a single unbroken curve.
exists or its graph is a single unbroken curve.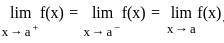
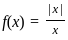
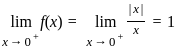
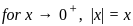
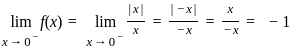

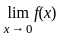
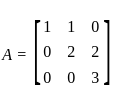
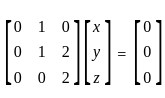

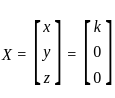
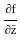 = 0.
= 0.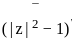 (∵|z|
(∵|z|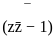
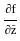 = 0
= 0
 and
and 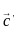 is denoted by
is denoted by 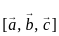 .
.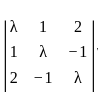 = 0
= 0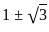
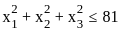 } is
} is 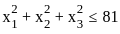 } represents the closed ball in
} represents the closed ball in 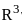 with radius 9 centered at the origin.
with radius 9 centered at the origin.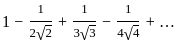 is
is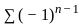 b
b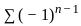 b
b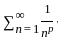 converges.
converges.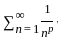 diverges.
diverges.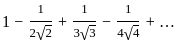
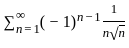
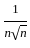 ≥ 0 ,
≥ 0 , 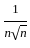 is decreasing
is decreasing 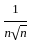 → 0 as n → ∞
→ 0 as n → ∞ 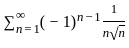 converges
converges 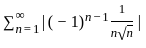 =
= 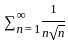
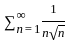 is convergent.
is convergent.










