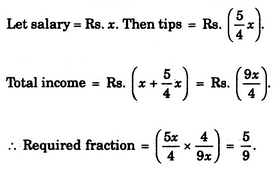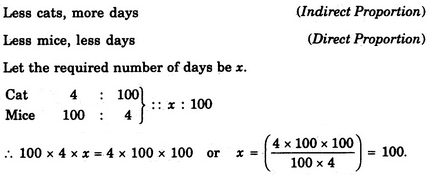परीक्षा: मात्रात्मक तर्क- 1 - RRB NTPC/ASM/CA/TA MCQ
25 Questions MCQ Test General Intelligence & Reasoning for RRB NTPC (Hindi) - परीक्षा: मात्रात्मक तर्क- 1
अमर, अकबर और एंथनी की उम्र का कुल योग 80 वर्ष है। तीन वर्ष पहले उनकी उम्र का कुल योग क्या था?
शहर A से B के लिए दो बस टिकट और शहर A से C के लिए तीन टिकट की कीमत 77 रुपये है, जबकि शहर A से B के लिए तीन टिकट और शहर A से C के लिए दो टिकट की कीमत 73 रुपये है। शहर B और C के लिए A से किराया क्या है?
कुछ दोस्तों ने पिकनिक पर जाने का निर्णय लिया और खाने-पीने पर 96 रुपये खर्च करने की योजना बनाई। हालांकि, उनमें से चार नहीं आए। इसके परिणामस्वरूप, बाकी लोगों को अतिरिक्त 4 रुपये देना पड़ा। पिकनिक में शामिल होने वाले लोगों की संख्या थी
एक संस्थान ने एक मेले का आयोजन किया और 1/5 लड़कियाँ और 1/8 लड़के ने इसमें भाग लिया। कुल छात्रों में से किस अंश ने मेले में भाग लिया?
A, B, C, D और E एक कार्ड का खेल खेलते हैं। A B से कहता है, 'यदि तुम मुझे तीन कार्ड देते हो, तो तुम्हारे पास E के जितने कार्ड होंगे और यदि मैं तुम्हें तीन कार्ड दूं, तो तुम्हारे पास D के जितने कार्ड होंगे।' A और B के पास मिलाकर D और E के पास से 10 कार्ड अधिक हैं। यदि B के पास C से दो कार्ड अधिक हैं और कुल कार्डों की संख्या 133 है, तो B के पास कितने कार्ड हैं?
एक अनानास की कीमत ₹7 है। एक तरबूज की कीमत ₹5 है। X इन फलों पर ₹38 खर्च करता है। खरीदे गए अनानासों की संख्या कितनी है?
एक महिला कहती है, "यदि आप मेरी उम्र को उल्टा कर दें, तो अंक मेरे पति की उम्र का प्रतिनिधित्व करते हैं। वह, निश्चित रूप से, मुझसे बड़े हैं और हमारी उम्र के बीच का अंतर उनके योग का एक ग्यारहवां हिस्सा है।" महिला की उम्र है
एक लड़की ने अपनी बाईं हाथ की अंगुलियों पर इस प्रकार गिनती की: उसने अंगूठे को 1, तर्जनी को 2, मध्य अंगुली को 3, अनामिका को 4, छोटी अंगुली को 5 कहा और फिर दिशा बदलते हुए अनामिका को 6, मध्य अंगुली को 7 और इसी तरह से आगे बढ़ा। उसने 1994 तक गिनती की। उसने किस अंगुली पर गिनती समाप्त की?
एक व्यक्ति के पास एक-रुपये, पांच-रुपये और दस-रुपये के नोटों में कुल Rs. 480 हैं। प्रत्येक श्रेणी के नोटों की संख्या समान है। उसके पास कुल कितने नोट हैं?
A, B से 3 वर्ष बड़ा है और C से 3 वर्ष छोटा है, जबकि B और D जुड़वाँ हैं। C, D से कितने वर्ष बड़ा है?
एक क्लब के 30 सदस्यों ने एक बैडमिंटन सिंगल्स टूर्नामेंट खेलने का निर्णय लिया। हर बार जब कोई सदस्य एक खेल हारता है, वह टूर्नामेंट से बाहर हो जाता है। कोई टाई नहीं होती। विजेता निर्धारित करने के लिए न्यूनतम मैचों की संख्या क्या होनी चाहिए?
एक बगीचे में, आम के पेड़ों की 10 पंक्तियाँ और 12 कॉलम हैं। दो पेड़ों के बीच की दूरी 2 मीटर है और बगीचे की सीमा से सभी ओर 1 मीटर की दूरी छोड़ दी जाती है। बगीचे की लंबाई क्या है?
12 वर्ष का मनिक अपने भाई राहुल से तीन गुना बड़ा है। मनिक राहुल से दो गुना बड़ा कब होगा?
एक दर्जी के पास कपड़े के एक रोल से काटने के लिए कई शर्ट के टुकड़े थे। उसने प्रत्येक रोल को समान लंबाई में 10 टुकड़ों में काटा। उसने प्रति मिनट 45 कट की गति से काटा। 24 मिनट में कितने रोल काटे जाएंगे?
60 छात्रों की कक्षा में, वार्षिक खेलों में भाग ले रहे लड़कों और लड़कियों की संख्या का अनुपात क्रमशः 3 : 2 है। खेलों में भाग नहीं ले रही लड़कियों की संख्या, भाग नहीं ले रहे लड़कों की संख्या से 5 अधिक है। यदि खेलों में भाग ले रहे लड़कों की संख्या 15 है, तो कक्षा में लड़कियों की कुल संख्या कितनी है?
जूलॉजिकल पार्क में हिरण और मोर हैं। सिरों की गिनती करते समय उनकी संख्या 80 है। उनके पैरों की संख्या 200 है। वहां कितने मोर हैं?
एक आदमी दो रंगों के मोजे पहनता है - काला और भूरा। उसके पास एक दराज में कुल 20 काले मोजे और 20 भूरे मोजे हैं। मान लीजिए कि उसे अंधेरे में मोजे निकालने हैं, तो उसे कितने मोजे निकालने होंगे ताकि यह सुनिश्चित हो सके कि उसके पास एक मेल खाने वाला जोड़ा है?
एक मोटर चालक के पास ब्रिस्टल से बर्मिंघम तक जाने के लिए चार अलग-अलग मार्ग हैं। बर्मिंघम से शेफील्ड तक जाने के लिए उसके पास तीन अलग-अलग मार्ग हैं और शेफील्ड से कार्लिस्ले तक जाने के लिए उसके पास दो अलग-अलग मार्ग हैं। ब्रिस्टल से कार्लिस्ले तक जाने के लिए उसके पास कुल कितने मार्ग हैं?
मैक्स के पास केन से £ 3 अधिक हैं, लेकिन फिर केन घोड़ों पर जीतता है और अपनी राशि को तीन गुना कर लेता है, जिससे उसके पास अब उन दोनों लड़कों के पास जो मूल राशि थी, उससे £ 2 अधिक है। केन की जीत से पहले मैक्स और केन के पास कुल कितना पैसा था?
कक्षा में 18 लड़के हैं जो 160 सेमी से अधिक ऊँचे हैं। यदि ये लड़कों का तीन-चौथाई भाग हैं और कुल लड़कों की संख्या कक्षा में कुल छात्रों का दो-तिहाई है, तो कक्षा में लड़कियों की संख्या क्या है?
एक पिता अब अपने बेटे की उम्र का तीन गुना है। पांच साल पहले, वह अपने बेटे की उम्र का चार गुना था। बेटे की उम्र (वर्षों में) है
एक वेटर का वेतन उसके वेतन और टिप्स से मिलकर बनता है। एक सप्ताह के दौरान उसकी टिप्स उसके वेतन का 5/4 थीं। उसकी कुल आय में से टिप्स का क्या भाग था?
यदि आप 1 से 100 तक सभी संख्याएँ लिखते हैं, तो आप 3 को कितनी बार लिखते हैं?
यदि 100 बिल्ली 100 चूहों को 100 दिनों में मारती हैं, तो 4 बिल्ली 4 चूहों को कितने दिनों में मारेंगी?
|
127 docs|197 tests
|
|
127 docs|197 tests
|



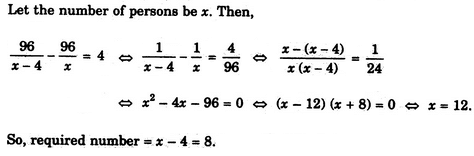
 5B = 125
5B = 125  B = 25।
B = 25।
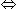 x = (4/5)y
x = (4/5)y