परीक्षा: मात्रात्मक तर्क - 3 - RRB NTPC/ASM/CA/TA MCQ
25 Questions MCQ Test General Intelligence & Reasoning for RRB NTPC (Hindi) - परीक्षा: मात्रात्मक तर्क - 3
एक छात्र ने उतने ही सवाल सही किए जितने उसने गलत किए। यदि उसने कुल 48 सवाल हल किए, तो उसने कितने सही हल किए?
डेविड एक इमारत के 11वें माले पर लिफ्ट में चढ़ता है और 57 मंजिल प्रति मिनट की दर से ऊपर जाता है। उसी समय, अल्बर्ट उसी इमारत के 51वें माले पर लिफ्ट में चढ़ता है और 63 मंजिल प्रति मिनट की दर से नीचे जाता है। यदि वे इन दरों पर यात्रा करना जारी रखते हैं, तो किस मंजिल पर उनके रास्ते मिलेंगे?
A, B, C और D एक कार्ड का खेल खेलते हैं। A B से कहता है, 'अगर मैं तुम्हें 8 कार्ड देता हूं, तो तुम्हारे पास C के समान कार्ड होंगे और मेरे पास C से 3 कम कार्ड होंगे। यदि मैं C से 6 कार्ड ले लूं, तो मेरे पास D से दो गुना कार्ड होंगे।' यदि B और D के पास कुल 50 कार्ड हैं, तो A के पास कितने कार्ड हैं?
मेरे पास कुछ मिठाइयाँ वितरित करने के लिए हैं। यदि मैं 2, 3 या 4 को एक पैक में रखता हूँ, तो मेरे पास एक मिठाई बचती है। यदि मैं 5 को एक पैक में रखता हूँ, तो मेरे पास कोई मिठाई नहीं बचती। मुझे पैक और वितरित करने के लिए न्यूनतम संख्या में मिठाइयाँ कितनी चाहिए?
गायों और मुर्गियों के एक समूह में, पैरों की संख्या सिरों की संख्या के दोगुने से 14 अधिक है। गायों की संख्या है
एक पिता अपने पुत्र से कहता है, 'मैं तुम्हारी वर्तमान आयु का था जब तुम पैदा हुए थे'। अगर पिता की उम्र अब 36 है, तो पुत्र की उम्र पाँच साल पहले कितनी थी?
A ने B के 3 शॉट्स के मुकाबले 5 शॉट्स फायर किए, लेकिन A केवल 3 शॉट्स में से एक बार ही शिकार करता है जबकि B 2 शॉट्स में से एक बार शिकार करता है। जब B ने 27 बार चूक की है, तब A ने कितने पक्षियों को मारा है?
एक कक्षा में, छात्रों का 3/5 लड़कियाँ हैं और बाकी लड़के हैं। यदि लड़कियों का 2/9 और लड़कों का 1/4 अनुपस्थित हैं, तो छात्रों की कुल संख्या में से कितने प्रतिशत छात्र उपस्थित हैं?
एक परिवार में, एक दंपति के एक पुत्र और एक पुत्री है। पिता की आयु उसकी पुत्री की आयु का तीन गुना है और पुत्र की आयु उसकी माँ की आयु का आधा है। पत्नी अपने पति से 9 वर्ष छोटी है और भाई अपनी बहन से सात वर्ष बड़ा है। माँ की आयु क्या है?
यदि 1 मिमी मोटी कागज को इस तरह मोड़ा जाए कि हर मोड़ पर क्षेत्रफल आधा हो जाए, तो 50 मोड़ों के बाद ढेर की मोटाई क्या होगी?
श्रीमान X, एक गणितज्ञ, एक संख्या को '6 से जुड़ी' के रूप में परिभाषित करते हैं यदि वह 6 से विभाज्य है या यदि उसके अंकों का योग 6 है, या यदि 6 उस संख्या में से एक अंक है। अन्य संख्याएँ सभी '6 से जुड़ी नहीं' हैं। इस परिभाषा के अनुसार, 1 से 60 (दोनों शामिल) तक की उन पूर्ण संख्याओं की संख्या जो 6 से जुड़ी नहीं हैं, यह है
वह संख्या खोजें जिसे स्वयं में 13 बार जोड़ने पर 112 मिलता है।
पहले गुच्छे में (1/4) दूसरी गुच्छे के बराबर केले हैं। यदि दूसरी गुच्छे में पहले गुच्छे से 3 केले कम हैं, तो पहले गुच्छे में केले की संख्या क्या है?
अरुणा ने एक केक को दो हिस्सों में काटा और एक आधे को समान आकार के छोटे टुकड़ों में काटा। प्रत्येक छोटे टुकड़े का वजन बीस ग्राम है। यदि उसके पास कुल सात टुकड़े हैं, तो मूल केक का वजन कितना था?
कुल 324 सिक्के 20 पैसे और 25 पैसे के हैं जिनका योग ₹71 है। 25 पैसे के सिक्कों की संख्या क्या है?
एक खिलाड़ी के पास चार प्रकार के 13 ताश के पत्ते होते हैं, जिनमें से सात काले और छह लाल होते हैं। वहाँ स्पेड्स की तुलना में हीरे की संख्या दो गुना है और हीरों की तुलना में दिल की संख्या दो गुना है। उसके पास कितने क्लब हैं?
एक शहर में टैक्सी चार्ज में एक निश्चित चार्ज और तय की गई दूरी का चार्ज शामिल होता है। 16 किमी की यात्रा के लिए, भुगतान की गई चार्ज Rs. 156 है और 24 किमी की यात्रा के लिए, भुगतान की गई चार्ज Rs. 204 है। 30 किमी की यात्रा के लिए व्यक्ति को कितना भुगतान करना होगा?
यदि हर 3 में से 2 रेडीमेड शर्टों के आस्तीन में सुधार की आवश्यकता होती है, और हर 5 में से 4 को शरीर में सुधार की आवश्यकता होती है, तो 60 शर्टों के लिए कितने सुधार की आवश्यकता होगी?
एक व्यापार सम्मेलन के अंत में उपस्थित दस लोग एक-दूसरे के साथ एक बार हाथ मिलाते हैं। कुल मिलाकर कितने हाथ मिलाने होंगे?
25 बच्चों के बीच मिठाइयाँ समान रूप से बाँटने के बाद, 8 मिठाइयाँ शेष रह जाती हैं। यदि बच्चों की संख्या 28 होती, तो समान वितरण के बाद 22 मिठाइयाँ बचती। कुल मिठाइयों की संख्या क्या थी?
1200 व्यक्तियों का एक समूह जिसमें कप्तान और सैनिक शामिल हैं, एक ट्रेन में यात्रा कर रहा है। हर 15 सैनिकों के लिए एक कप्तान है। समूह में कप्तानों की संख्या कितनी है?
एक गाड़ी में, 50 मुर्गियों के अलावा, 45 बकरियां और 8 ऊंट हैं, जिनके साथ कुछ रखवाले हैं। यदि गाड़ी में कुल पैरों की संख्या सिरों की संख्या से 224 अधिक है, तो रखवालों की संख्या कितनी है?
एक बंदर हर घंटे की शुरुआत में 30 फीट चढ़ता है और फिर आराम करता है, जब वह पीछे की ओर 20 फीट फिसल जाता है, फिर वह अगले घंटे की शुरुआत में चढ़ाई फिर से शुरू करता है। यदि वह सुबह 8:00 बजे अपनी चढ़ाई शुरू करता है, तो वह जमीन से 120 फीट ऊँचे ध्वज को पहले कब छुएगा?
एक संख्या दो अंकों की है जिनका योगफल 11 है। यदि संख्या में 27 जोड़ा जाए, तो अंकों की स्थिति बदल जाती है। वह संख्या क्या है?
एक उद्यमी व्यवसायी पहले दिन में 1 रुपये की आय अर्जित करता है। हर अगले दिन, उसकी आय पिछले दिन की आय का दोगुना होती है। व्यवसाय के 10वें दिन, उसकी आय कितनी होगी?
|
127 docs|197 tests
|
|
127 docs|197 tests
|


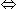 3x = 48
3x = 48 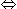 x = 16।
x = 16।

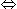 4x + 2y = 2x + 2y + 14
4x + 2y = 2x + 2y + 14 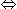 2x = 14
2x = 14 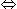 x = 7।
x = 7।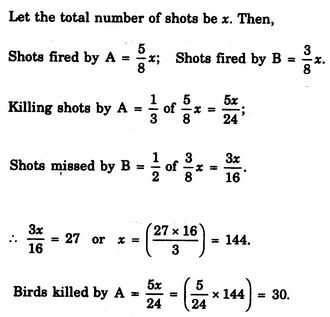


 20x + 25(324 - x) = 7100
20x + 25(324 - x) = 7100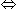 5x = 1000
5x = 1000 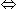 x = 200। इस प्रकार, 25 पैसे के सिक्कों की संख्या = (324 - x) = 124 होगी।
x = 200। इस प्रकार, 25 पैसे के सिक्कों की संख्या = (324 - x) = 124 होगी।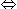 6x = 6
6x = 6 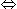 x - 1।
x - 1।
 28x - (3x + 14) 28 से विभाज्य है।
28x - (3x + 14) 28 से विभाज्य है। x = 14।
x = 14।
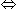 9x + 38 = 110 - 9x
9x + 38 = 110 - 9x 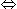 18x = 72
18x = 72 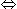 x = 4।
x = 4।










