All Courses
Get the App Signup / Login
Sign in Open App
JEE Exam  >  JEE Tests  >  WBJEE Sample Papers, Section Wise & Full Mock Tests 2025  >  WBJEE Maths Test - 8 - JEE MCQ

WBJEE Maths Test - 8 - JEE MCQ


Test Description

30 Questions MCQ Test WBJEE Sample Papers, Section Wise & Full Mock Tests 2025 - WBJEE Maths Test - 8

WBJEE Maths Test - 8 for JEE 2024 is part of WBJEE Sample Papers, Section Wise & Full Mock Tests 2025 preparation. The WBJEE Maths Test - 8 questions and answers have been prepared according to the JEE exam syllabus.The WBJEE Maths Test - 8 MCQs are made for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for WBJEE Maths Test - 8 below.
Solutions of WBJEE Maths Test - 8 questions in English are available as part of our WBJEE Sample Papers, Section Wise & Full Mock Tests 2025 for JEE & WBJEE Maths Test - 8 solutions in Hindi for WBJEE Sample Papers, Section Wise & Full Mock Tests 2025 course. Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt WBJEE Maths Test - 8 | 75 questions in 120 minutes | Mock test for JEE preparation | Free important questions MCQ to study WBJEE Sample Papers, Section Wise & Full Mock Tests 2025 for JEE Exam | Download free PDF with solutions
WBJEE Maths Test - 8 - Question 1
Save

In the expansion of 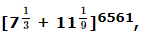  the number of terms free from radicals is

Detailed Solution for WBJEE Maths Test - 8 - Question 1

General term,

are integers for
0 ≤ r ≤ 6561
∴ r = 0, 9, 18, 27, ...6561
0, 9, 18, ...6561 is in A.P.
First term, a = 0
Common - difference = 18 - 9 = 9
Last term, t = 6561
l = a + (n - 1)d, where n = number of terms
⇒ 6561 = 0 + (n - 1)9
⇒ 9(n - 1) = 6561
⇒ n - 1 = 729
⇒ n = 729 + 1
⇒ n = 730

WBJEE Maths Test - 8 - Question 2
Save

The coefficient of x-9 in the expansion of ((x2/2) - (2/x))9 is

1 Crore+ students have signed up on EduRev. Have you? Download the App
WBJEE Maths Test - 8 - Question 3
Save

The coefficient of x3 in ((√x5) + (3/√x3))6 is

WBJEE Maths Test - 8 - Question 4
Save
Equation x2+2ax-b2=0 has real roots α , β and equation x2+2px-q2=0 has real roots γ , δ . If the circle C is drawn with the points ( α , γ ), ( β , δ ) as extremities of a diameter, then the equation of C is
WBJEE Maths Test - 8 - Question 5
Save

The equation of circle which passes through (4,5) and whose centre is (2,2) is
WBJEE Maths Test - 8 - Question 6
Save

If the cube roots of unity are 1,ω,ω2 then the roots of the equation (x - 2)3+27 = 0 are
WBJEE Maths Test - 8 - Question 7
Save
Let z1 and z2 be two complex numbers whose principle argument are α and β then, arg (z1.z2) =
Detailed Solution for WBJEE Maths Test - 8 - Question 7
Let z1 and z2 have polar representations z1 = r1( cos α + isinα)
and z2 = r2 (cosβ + isinβ ).
Then z1 z2 = r1 (cosα+i sinα) r2 (cosβ + isinβ )
= r1 r2 (cosαcosβ − sinαsinβ) + i(cosαsinβ + sinαcosβ )
= r1 r2 (cos (α+β ) + isin (α+β )),
which is the polar representation of z1 z2 , as r1 r2 = |z1 ||z2 |=|z1 z2 |.
Hence α+β is an argument of z1 z2
WBJEE Maths Test - 8 - Question 8
Save

If m and n are integers, then what is the value of sin mx sin nxdx . If m ≠ n
Detailed Solution for WBJEE Maths Test - 8 - Question 8

Since sin mx, sin nx is an odd function if m ≠ n, then  sin mx . sin nx dx = 0

WBJEE Maths Test - 8 - Question 9
Save

WBJEE Maths Test - 8 - Question 10
Save

WBJEE Maths Test - 8 - Question 11
Save

WBJEE Maths Test - 8 - Question 12
Save

WBJEE Maths Test - 8 - Question 13
Save

The area bounded by the parabola y2=4ax and the straight line y=2ax is
Detailed Solution for WBJEE Maths Test - 8 - Question 13


WBJEE Maths Test - 8 - Question 14
Save

The solution of the differential equation 2xy(dy/dx)=x2+3y2 is (where c is a constant)
WBJEE Maths Test - 8 - Question 15
Save

What is the solution of x2y2dy = (1−xy3) dx?
WBJEE Maths Test - 8 - Question 16
Save

If
then f ′(1) =
WBJEE Maths Test - 8 - Question 17
Save

The curve represented by x = 2(cos t + sin t), y = 5 (cos t - sin t) is
WBJEE Maths Test - 8 - Question 18
Save

The eccentric angles of the extremities of the latus-rectum intersecting positive x-axis of the ellipse ((x2/a2) + (y2/b2) = 1) are given by
WBJEE Maths Test - 8 - Question 19
Save

If

Detailed Solution for WBJEE Maths Test - 8 - Question 19

WBJEE Maths Test - 8 - Question 20
Save

The slopes of the common tangents to the hyperbola x2/y - y2/16 = 1 and y2/9 - x2/16 = 1 are
WBJEE Maths Test - 8 - Question 21
Save
The foci of the hyperbola 9x2 - 16y2 + 18x + 32y - 151 = 0 are
WBJEE Maths Test - 8 - Question 22
Save

The function is increasing in
WBJEE Maths Test - 8 - Question 23
Save

The value of cos⁻1(cos 5π/3) + sin⁻1 (sin 5π/3) is
WBJEE Maths Test - 8 - Question 24
Save

is equal to
Detailed Solution for WBJEE Maths Test - 8 - Question 24

WBJEE Maths Test - 8 - Question 25
Save

The system of linear equation x + y + z = 2, 2x + y - z = 3, 3x + 2y + kz = 4 has a unique solution, then
Detailed Solution for WBJEE Maths Test - 8 - Question 25

Augmented matrix is



∴ Given system of equations has a unique solution ⇒ k ≠ 0

WBJEE Maths Test - 8 - Question 26
Save

For all real x, the minimum value of (1 - x + x2)/(1 + x + x2) is
WBJEE Maths Test - 8 - Question 27
Save
If the vertices O,A,B of any equilateral triangle are situated at z=0, z=z₁ and z=z₂ respectively, then which of the following are true ?
WBJEE Maths Test - 8 - Question 28
Save
Which of the following points lie on the parabola x2=4ay ?
WBJEE Maths Test - 8 - Question 29
Save

The length of the normal chord to the parabola y2 = 4x which subtends a right angle at the vertex is
Detailed Solution for WBJEE Maths Test - 8 - Question 29


Again AB subtends a right angle at the vertex O (0, 0) of the parabola

WBJEE Maths Test - 8 - Question 30
Save
P,Q,R and S have to deliver lecture, then in how many ways can the lectures be arranged?
Detailed Solution for WBJEE Maths Test - 8 - Question 30
Total no. of ways delivering lectures = 4P4 = 4! = 24
View more questions
3 videos|10 docs|54 tests
Join Course
Information about WBJEE Maths Test - 8 Page
In this test you can find the Exam questions for WBJEE Maths Test - 8 solved & explained in the simplest way possible. Besides giving Questions and answers for WBJEE Maths Test - 8, EduRev gives you an ample number of Online tests for practice

Top Courses for JEE

Download as PDF

Top Courses for JEE

Important Questions for WBJEE Maths Test - 8

Find all the important questions for WBJEE Maths Test - 8 at EduRev.Get fully prepared for WBJEE Maths Test - 8 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the WBJEE Maths Test - 8 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of WBJEE Maths Test - 8 resources.

WBJEE Maths Test - 8 MCQs with Answers

Prepare for the WBJEE Maths Test - 8 within the JEE exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for WBJEE Maths Test - 8 WBJEE Sample Papers, Section Wise & Full Mock Tests 2025

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace WBJEE Maths Test - 8 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup