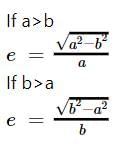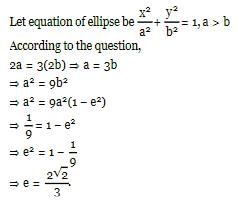WBJEE Maths Test - 1 - JEE MCQ
30 Questions MCQ Test - WBJEE Maths Test - 1
If the coefficient of x7 in [ax2+(1/bx)]11 equals the coefficient of x-7 in [ax-(1/bx2)]11, then a and b satisfy the relation
The third term in the expansion of ((x2) - (1/x3))n is independent of x, when n is equal to
The equation of the circle passing through intersection of circles x2+y2-1=0 and x2+y2-2x-4y+1=0 and touching x+2y=0 is
The equation of circle which passes through (4,5) and whose centre is (2,2) is
The area bounded by the ellipse x2+9y2=9 and the straight line x+3y=3 is
The degree of the differential equation d2y/dx2+(dy/dx)3+6y=0 is
The graph represented by the equations x = sin2t,y = 2cost is
If the major axis of an ellipse is thrice the minor axis, then its eccentricity is equal to
The curve represented by x = a (coshθ + sinhθ) , y = b(coshθ − sinhθ) is
The least possible value of k for which the function f(x) = x2 + kx + 1 may be increasing on [1,2] is
αx+y+z = α-1
x+αy+z = α-1
x+y+αz, = α-1 has no solution, if α is
The equation of the parabola whose vertex is at (2,-1) and focus at (2,-3) is
The pole of the line 2x + 3y − 4 = 0 with respect to the parabola y2 = 4x is
How many total words can be formed from the letters of the word INSURANCE in which vowels are always together?