BITSAT Mock Test - 1 - JEE MCQ
30 Questions MCQ Test - BITSAT Mock Test - 1
A particle of charge q moves with a velocity  m/s in a magnetic field
m/s in a magnetic field 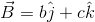 T, where a, b and c are constants. The magnitude of the force experienced by the particle is
T, where a, b and c are constants. The magnitude of the force experienced by the particle is
 m/s in a magnetic field
m/s in a magnetic field 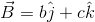 T, where a, b and c are constants. The magnitude of the force experienced by the particle is
T, where a, b and c are constants. The magnitude of the force experienced by the particle isA man is swimming perpendicular to a river with a constant acceleration (in y direction). The river is flowing with a constant velocity in x direction. The trajectory of the man as seen from the ground is
Two coils A and B, each of 10 turns and radius 20 cm, are held such that coil A lies in the vertical plane and coil B in the horizontal plane with their centres coinciding. What current should be passed through the coils so as to nullify Earth's magnetic field at their common centre?
(Given: Horizontal component of Earth's field = 0.314 x 10-4 T, angle of dip = 26.6o and tan 26.6o = 0.5)
(Given: Horizontal component of Earth's field = 0.314 x 10-4 T, angle of dip = 26.6o and tan 26.6o = 0.5)
The height of a solid cylinder is four times its radius. It is kept vertically at time t = 0 on a belt, which is moving in the horizontal direction with a velocity v = 2.45 t2, where v is in ms–1 and t is in seconds. If the cylinder does not slip, then it will topple over at time t equal to
If g is the acceleration due to gravity on the surface of the Earth, then the gain in potential energy of an object of mass m raised from the Earth's surface to a height equal to the radius R of the earth is
Two point charges q1 = 2μC and q2 = 1μC are placed at distances b = 1 cm and a = 2 cm from the origin on the y-axis and x-axis as shown in the figure. The electric field vector at point P(a, b) will subtend an angle θ with the x-axis given by
The magnetic field at the centre of a circular coil of radius r and carrying a current I is B. What is the magnetic field at a distance x =√3r from the centre on the axis of the coil?
A tank is filled with water of density 1 g/cm3 and oil of density 0.9 g/cm3. The height of water layer is 100 cm and that of oil layer is 400 cm. If g = 980 cm/s2, then the velocity of efflux from an opening in the bottom of the tank will be
If 0.1 M of a weak acid is taken and its percentage of degree of ionisation is 1.34%, then its ionisation constant will be
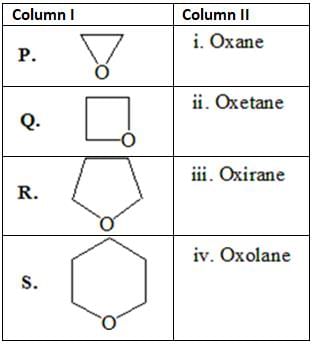
Compare the acidic strengths of the following carboxylic acids:
(i) PhCOOH
(ii) o-NO2C6H4COOH
(iii) p-NO2C6H4COOH
(iv) m-NO2C6H4COOH
Which of the following orders is correct?
Directions: In the following question, some part of the sentence may have an error of grammar or syntax. Find out which part of the sentence has the error and choose the correct option. If the sentence is free from errors, "No error" is the answer.
I was surprised (A)/ when the hostess smiled (B)/ as if she saw me before. (C)/ No error (D)
Directions: Find the wrong term in the following series.
49, 49, 50, 54, 60, 79, 104
Directions: In the following question, there is a certain relationship between the two terms given to the left of the sign (: :). The same relationship exists between the two terms to its right, out of which one is missing. Find the missing term from the given alternatives.
RSQ : UVT : : XYW : ?
From the given alternatives, find the correct relationship that holds between two terms:
FJUL : BOQQ :: LHRX : _________
Directions: Select the related number from the given alternatives.
36 : 216 : : 81 : ?
Directions: Select the one which best expresses the same sentence in passive/active voice.
His pocket has been picked.
If the number of terms in the expansion of (x - 2y + 3z)n is 45, then what is the value of n?
If θ is an acute angle and sin θ/2 = √[(x - 1) / 2x)], then tan θ is equal to
If the focal chord of y2 = 16x is tangent to (x - 6)2 + y2 = 2, then the possible values of slope of the given chord is
There are n different books and m copies of each in a college library. The number of ways in which a selection of one or more books can be done is
The area of the triangle formed by the line x + y = 3 and the angle bisector of the pair of lines x2 - y2 + 2y = 1 is
How many words can be formed by taking four different letters of the word MATHEMATICS?
The solution curves of the differential equation (xdx + ydy) √(x2 + y2) = (xdy - ydx) (√(1 - x2 - y2)) are


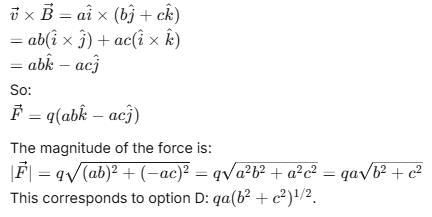
 and velocity of the person w.r.t. river
and velocity of the person w.r.t. river 

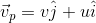
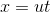 ------1
------1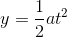 ----- 2, where a is the acceleration of the person
----- 2, where a is the acceleration of the person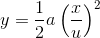




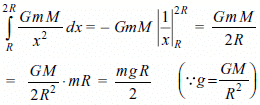





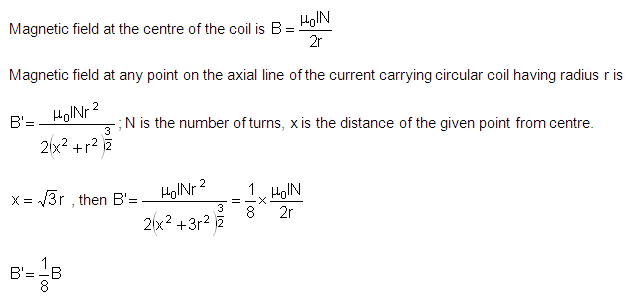
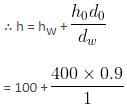
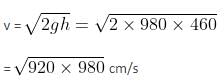
 , where Ka = Equilibrium constant for weak acid
, where Ka = Equilibrium constant for weak acid
 10-2)2
10-2)2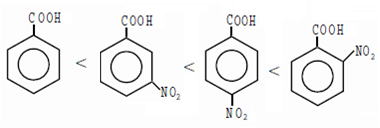
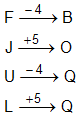

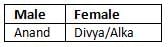
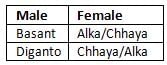
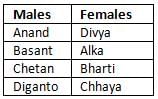
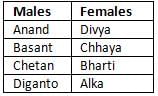
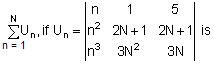
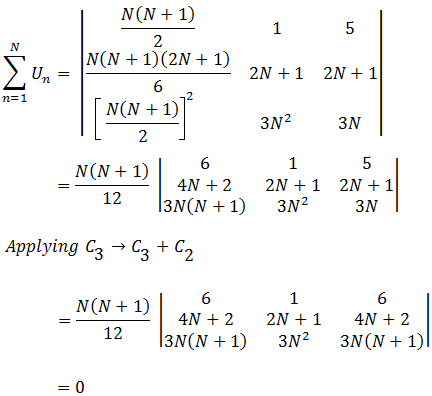
 , then
, then











