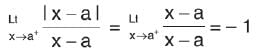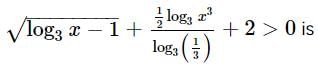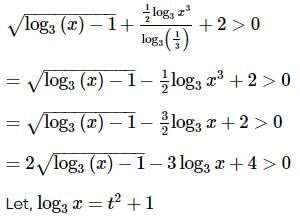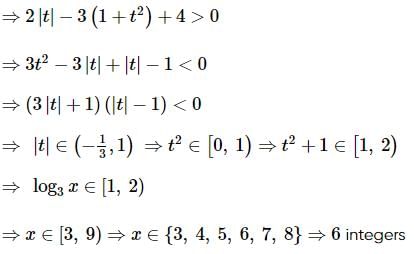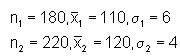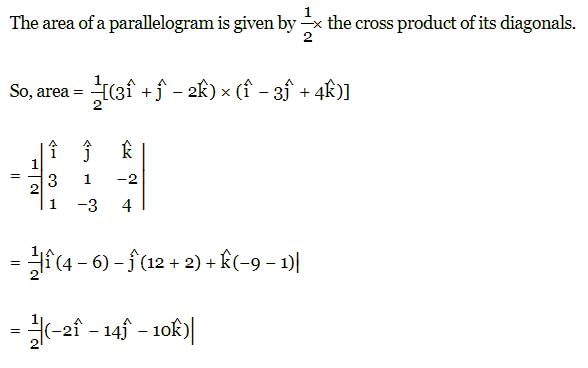VITEEE Maths Test - 6 - JEE MCQ
30 Questions MCQ Test - VITEEE Maths Test - 6
If a > 0, then the expression ax2 + bx + c is positive for all values of 'x' provided
Consider 50 consecutive integers starting from 11. What is the value of variance of these integers?
If f (x) = log5 + log (x3 - 3), where x [-1, 1], then find the value of c by using Rolle's theorem.
A manager draws two pens from his drawer randomly and one by one. The drawer has three blue and three red pens. What is the probability that both of them are of different colours?
Let P, Q and R be the interior angles of a triangle PQR. What is the value of 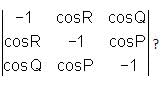
Which of the following equations is satisfied by the given function?
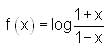
A tangent of a curve intercepts the y-axis at a point P, which is perpendicular to the tangent through another point (3, 1) on the curve. The differential equation of this curve is
If this scalar triple product of three non-zoro vectors is zero, then the vectors are
The area of triangle formed by the lines y = x, y = 2x and y = 3x + 4 is
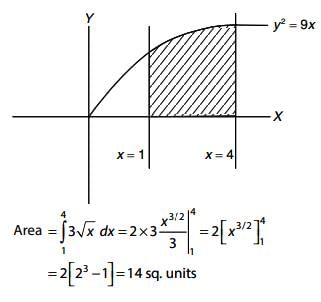
The area bounded by the curve y2 = 9x and the lines x = 1, x = 4 and y = 0 in the first quadrant is
If F1 ≡ (0, 0), F2 ≡ (3, 4) and I PF1I + IPF2l = 10, then locus of p is
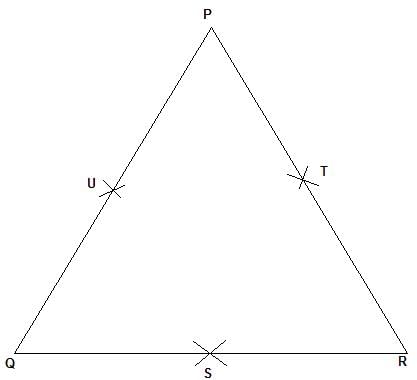
The mid-points of sides QR, RP and PQ of a triangle PQR are (p, 0, 0), (0, q, 0) and (0, 0, r). What is the value of 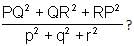
Directions: Consider the given lines.
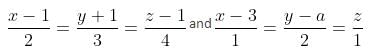
If L1 and L2 intersect at any point, then what is the value of a?
The SD and mean of a sample of 180 data are 6 and 110, respectively. Also, SD and the mean of another group of 220 data are 4 and 120, respectively. What is the value of combined variance of all the data?
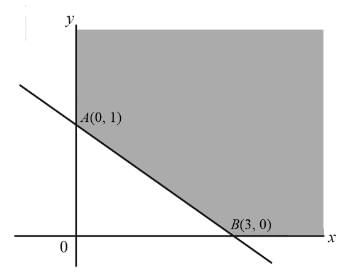
The area of the feasible region for the following constraints 3y + x ≥ 3, x ≥ 0, y ≥ 0 will be
The area of the parallelogram, whose digonal are given by the vectors, is
is


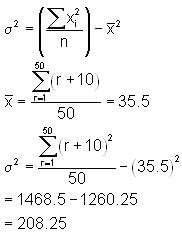

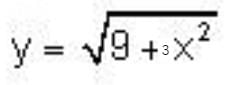 and
and 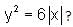
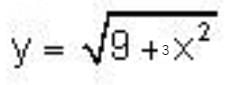
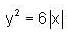
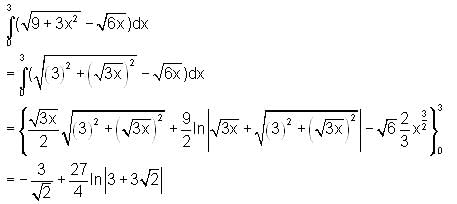
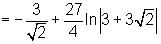
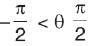
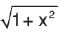
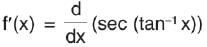
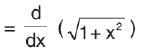
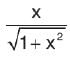
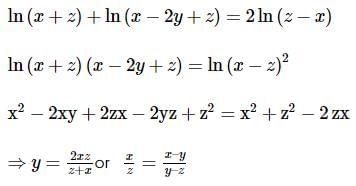
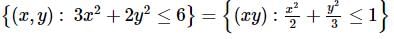
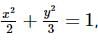 so this is a convex set.
so this is a convex set. 
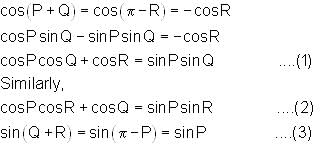
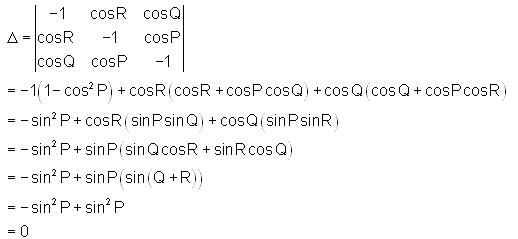
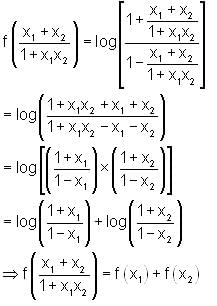
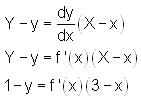
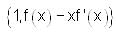

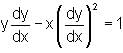



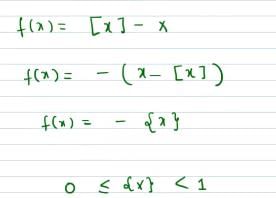
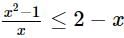 is
is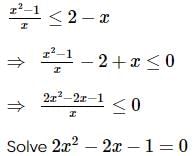
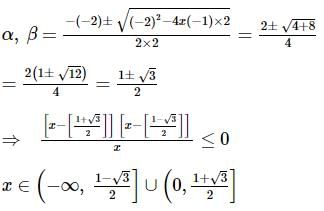
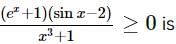
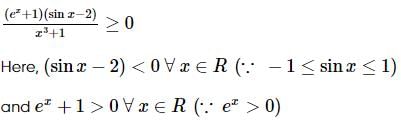
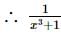 must be less than zero to satisfy the given inequality.
must be less than zero to satisfy the given inequality.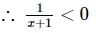
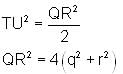
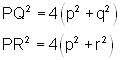

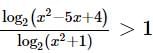 is
is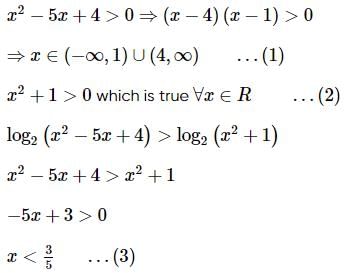
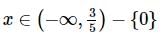
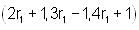 and on L2 is
and on L2 is 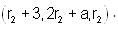

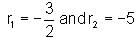
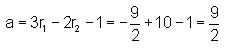
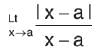 for x>a
for x>a