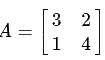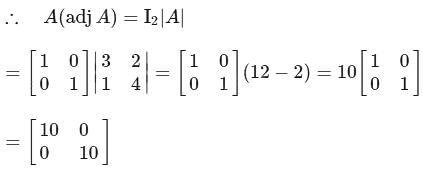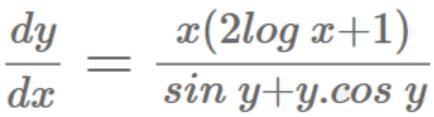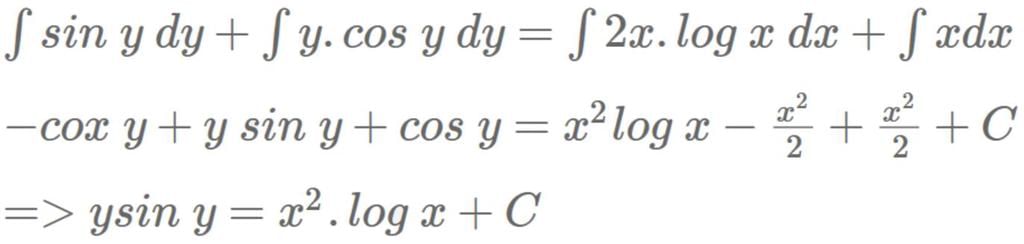VITEEE Maths Test - 3 - JEE MCQ
30 Questions MCQ Test - VITEEE Maths Test - 3
The centre of sphere passing through four points (0, 0, 0), (0, 2, 0), (1, 0, 0) and (0, 0, 4) is
The area bounded by the curve  and the
and the 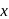 -axis, where
-axis, where 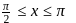 , is equal to
, is equal to
 and the
and the 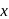 -axis, where
-axis, where 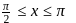 , is equal to
, is equal toThe graph of y = logax is reflection of the graph of y = ax in the line
If 0 ≤ x ≤ π and 81 sin²(x) + 81 cos²(x) = 30, then what is the value of x?
From the top of the house 15 metres high the angle of depression of a point which is at a distance 15 m from the base of the house is
The circles x2 + y2 - 12x -12y = 0 and x2 + y2 + 6x + 6y = 0
The coefficient of x-9 in the expansion of ((x2/2) - (2/x))9 is
Length of tangent drawn from (5,1) to the circle x2 + y2 + 6x - 4y - 3 = 0 is
How many even numbers can be formed by using all the digits 2, 3, 4, 5, 6?
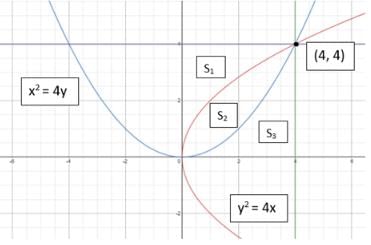
The parabolas y2 = 4x and x2 = 4y divide the square region bounded by the lines x = 4, y = 4 and the coordinate axes. If S₁, S₂, S₃ are respectively the areas of these parts numbered from top to bottom; then S₁ : S₂ : S₃ is
A six-faced dice is so biased that it is twice as likely to show an even number as an odd number when thrown. It is thrown twice. The probability that the sum of two numbers thrown is even is
The solution of the differential equation cos x sin y dx + sin x cos y dy = 0 is
Let Aand B be two matrices of order n×n. Let A be non-singular and B be singular. Consider the following:
1. AB is singular
2. AB is non-singular
3. A−1 B is singular
4. A−1 B is non singular Which of the above is/ are correct?
The differential equation of the family of lines through the origin is
The slope of the tangent of the curve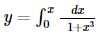 at the point where x = 1 is
at the point where x = 1 is
The ratio in which the line joining the points (a,b,c) and (-a,-c,-b) is divided by the xy-plane is
The solution of differential equation (dy/dx) = [(x(2logx + 1)) / (siny + ycosy)] is
Out of 6 boys and 4 girls a group of 7 is to be formed. In how many ways can this be done if the group is to have a majority of boys?
The third term of a G.P. is 3. The product of its first five terms is


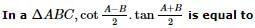
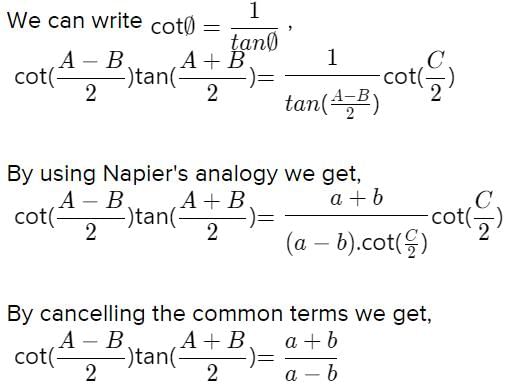

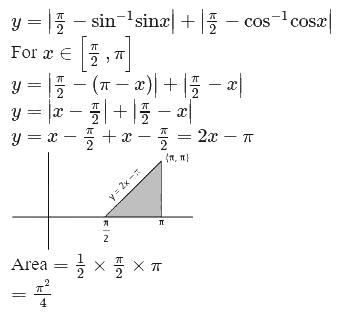
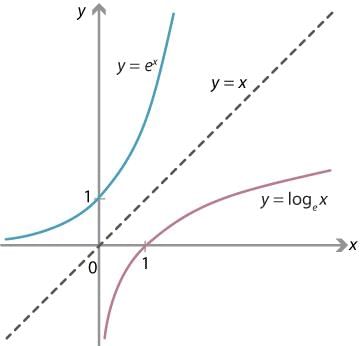
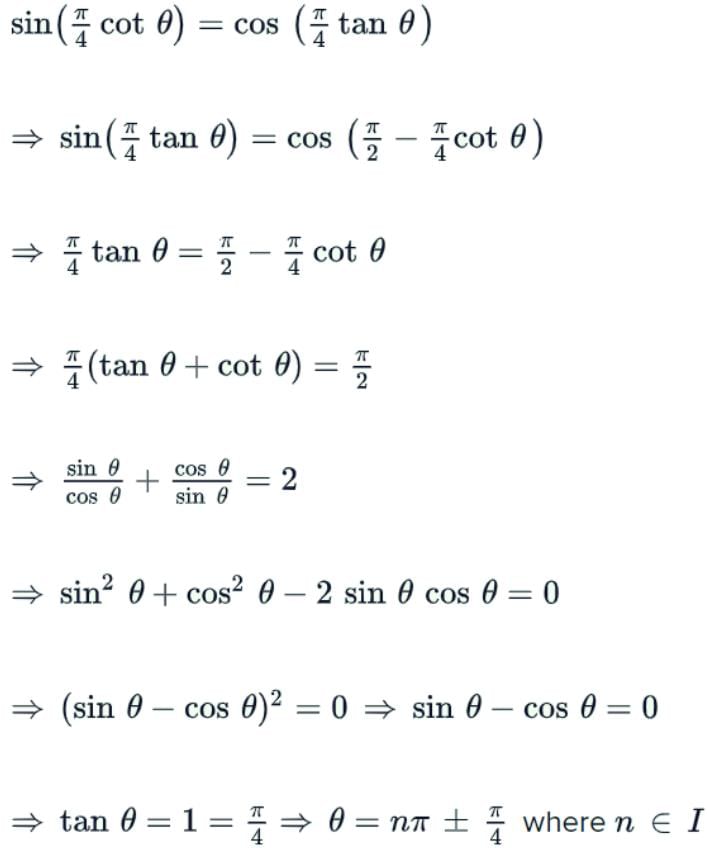

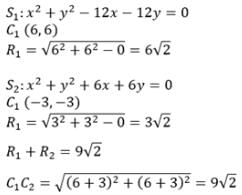
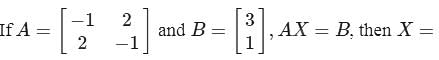
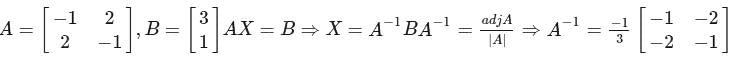
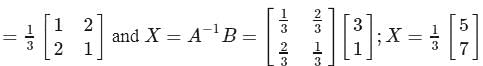
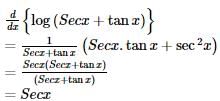
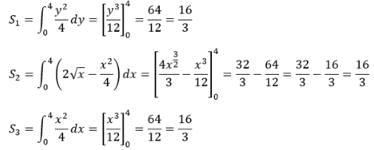
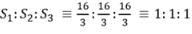
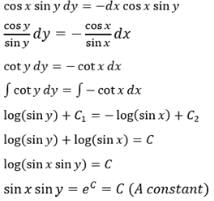
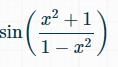 , find dy/dx
, find dy/dx
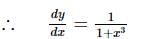

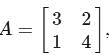 then what is A(adj A) equal to
then what is A(adj A) equal to