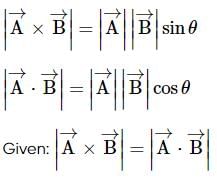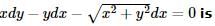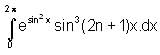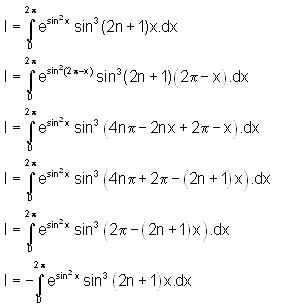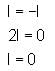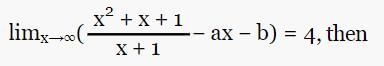VITEEE Maths Test - 9 - JEE MCQ
30 Questions MCQ Test - VITEEE Maths Test - 9
Consider the given expression:
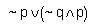
The negation of the above expression is
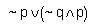
The angle between 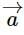 and
and 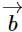 is
is 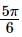 and the projection of
and the projection of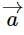 in the direction of
in the direction of 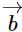 is
is 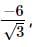 then
then 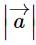 is equal to
is equal to
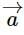 and
and 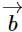 is
is 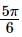 and the projection of
and the projection of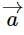 in the direction of
in the direction of 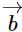 is
is 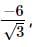 then
then 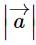 is equal to
is equal toThe locus of the point of intersection of two normals to the parabola x2=8y, which are at right angles to each other,is
The equation of the parabola with its vertex at (1,1) and focus at (3,1) is
The length of the shadow of a rod inclined at 10o to the vertical towards the sun is 2.05 metres when the elevation of the sun is 38o.The length of the rod is
The product of the perpendicular, drawn from any point on a hyperbola to its asymptotes is
A and B are square matrices of order n x n, then (A - B)2 is equal to
The equation of the line parallel to the tangent to the circle x2 + y2 = r2 at the point (x₁, y₁) and passing thro' origin is
If equation λx2 + 2y2 - 5xy + 5x - 7y + 3 = 0, represents two straight lines, the value of λ is
If the co-ordinates of the points A,B,C be (−1, 3, 2), (2, 3, 5) and (3, 5,−2) respectively, then ∠A=
The area bounded by the curve x = at2, y = 2at and the X-axis is 1 ≤ t ≤ 3 is
If α + i β = tan⁻1 z, z = x + yi and α is constant, then locus of \'z\' is
The value of b such that the scalar product of the vector î+ĵ+k̂ with the unit vector parallel to the sum of the vectors 2î + 4ĵ - 5k̂ and bî+ 2ĵ + 3k̂ is one is
Four normal dice are rolled once. The number of possible outcomes in which at least one die shows up 2 is -


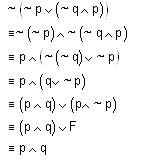
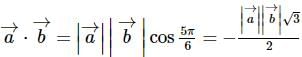
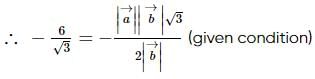
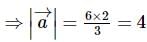

 is a unit vector, then
is a unit vector, then 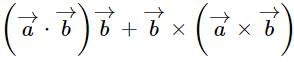 is
is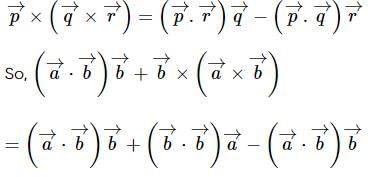
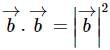
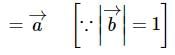


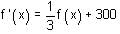 and f (0) = 300 , then find f(x).
and f (0) = 300 , then find f(x).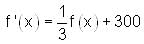
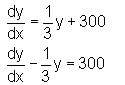
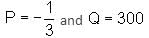
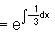
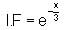
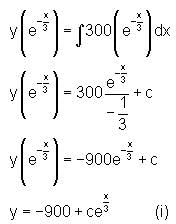
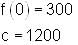
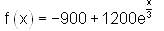
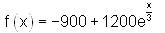

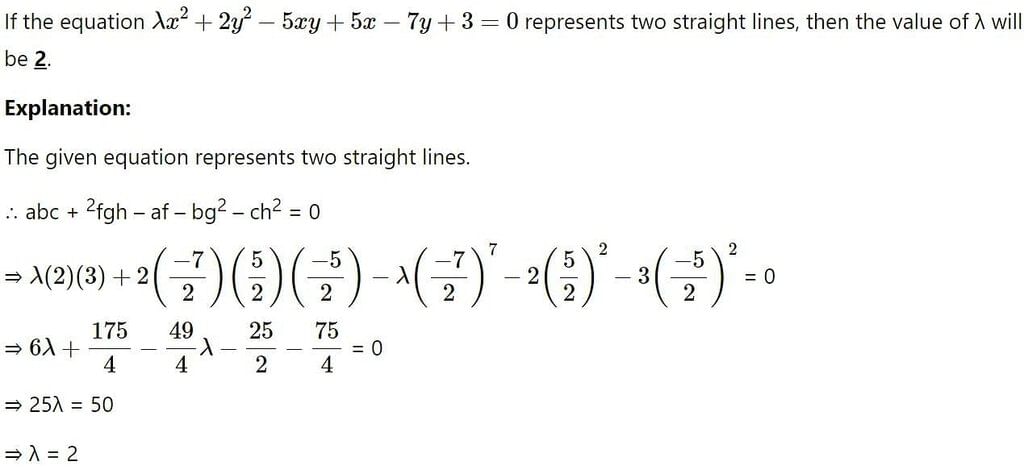
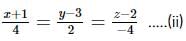
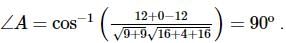
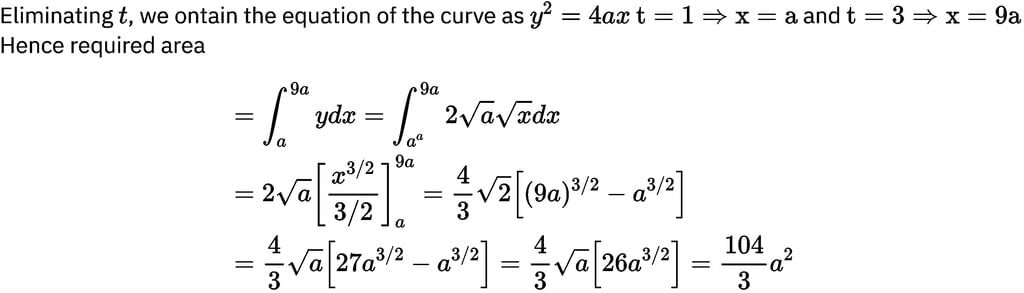
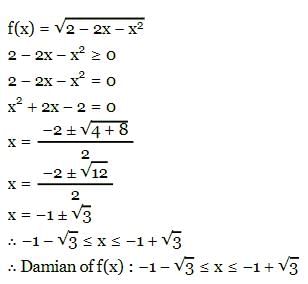
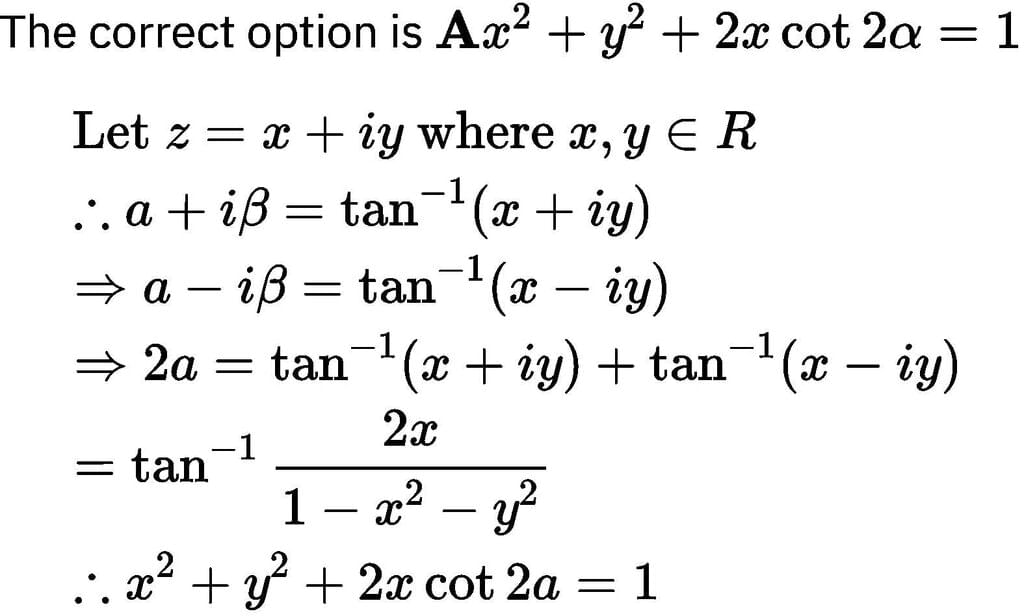
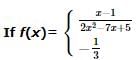
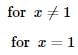
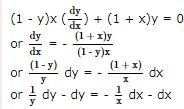
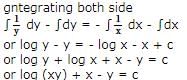
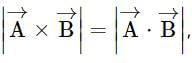 then angle between the vectors
then angle between the vectors  and
and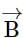 is
is