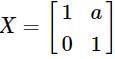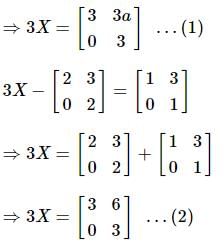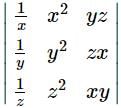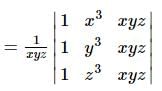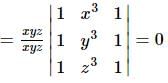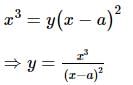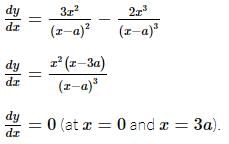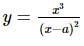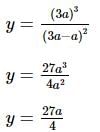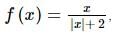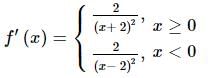SRMJEE Mock Test - 4 (Engineering) - JEE MCQ
30 Questions MCQ Test - SRMJEE Mock Test - 4 (Engineering)
Earth is assumed to be a sphere of radius R. A platform is arranged at a height R from the surface of Earth. The escape velocity of a body from this platform is fve, where ve is its escape velocity from the surface of Earth. The value of f is
What is the weight of a body at a distance 2r from the centre of Earth if the gravitational potential energy of the body at a distance r from the centre of Earth is U?
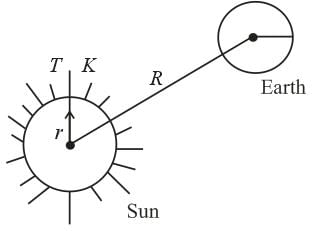
Assuming the sun to have a spherical outer surface of radius r, radiating like a black body at temperature t°C. The power received by a unit surface, (normal to the incident rays) at a distance R from the centre of the sun is
(σ is the Stefan's constant.)
(σ is the Stefan's constant.)
A body of mass 10 kg is acted upon by two perpendicular forces, 6 N and 8 N. The resultant acceleration of the body is:
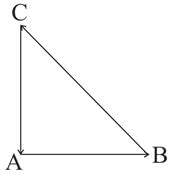
Three forces start acting simultaneously on a particle moving with velocity 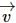 . These forces are represented in magnitude and direction by the three sides of triangle ABC (as shown). The particle will now move with velocity
. These forces are represented in magnitude and direction by the three sides of triangle ABC (as shown). The particle will now move with velocity
Light of wavelength 4000 Å incident on a sodium surface for which the threshold wavelength of photoelectrons is 5420 Å. The work function of sodium is
In a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.14s. the frequency of the wave is
When two waves with the same frequency and constant phase difference interfere
A square loop is made by a uniform conductor wire as shown in figure
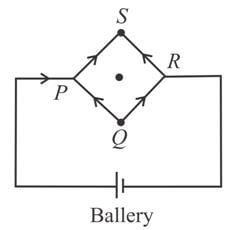
The net magnetic field at the centre of the loop if side length of the square is a
In a surface tension experiment with a capillary tube, water rises upto 0.1 m. If the same experiment is repeated in an artificial satellite, which is revolving around the Earth, water will rise in the capillary tube upto a height of
A ball is moving in a circular path of radius 5 m. If the tangential acceleration at any instant is 10 m/s² and the net acceleration makes an angle of 30° with the centripetal acceleration, then the instantaneous speed is:
Consider the following half reactions:
Zn2+ + 2e- → Zn(s); E0 = -0.76V
Cu2+ + 2e- → Cu(s); E0 = -0.34V
Which of the following reactions is spontaneous?
The β glucose and α glucose have different specific rotations. When either is dissolved in water, their rotation changes until the same fixed value results. This is called
Reagents that convert acetophenone into the following alcohol are
Which one of the following compounds will be most readily attacked by an electrophile?
When HCl gas is passed through a saturated solution of BaCl₂, a white precipitate is obtained. This is due to:
For the reaction: Cl₂ + 2I⁻ → I₂ + 2Cl⁻ The initial concentration of I⁻ was 0.20 mol L⁻¹, and after 20 minutes, the concentration remained 0.20 mol L⁻¹. Then, the rate of formation of I₂ in mol L⁻¹ min⁻¹ would be:
Transition metals do not show the highest oxidation state with fluorine, but they do so with oxygen. What would be the proper reason for the same?
If x, y, z are non zero real numbers, then the values of 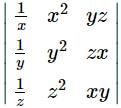 depends upon
depends upon
The coordinates of the point on the curve x³ = y(x - a)², where the ordinate is minimum, is
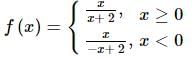
The number of points at which f(x) = x / |x| + 2 is non-differentiable is:
A sum of money becomes 7/4 of itself in 6 years at a certain rate of simple interest. Find the rate of interest.
A water pipe is cut into two pieces. The longer piece is 70% of the length of the pipe. By how much percentage is the longer piece longer than the shorter piece?
If x − 1/x = 5, then find the value of x⁴ + 1/x⁴.


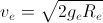
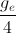 .
.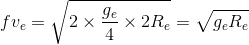
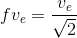

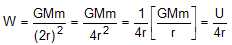

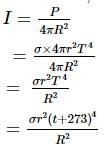
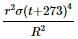
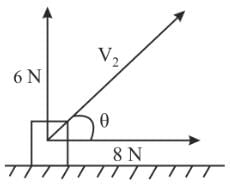
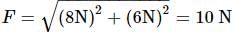
 = 1 m/s2
= 1 m/s2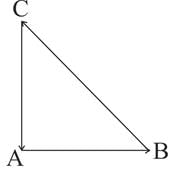
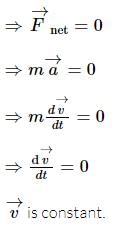
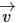 remains unchanged.
remains unchanged.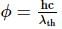
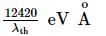
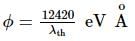
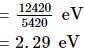
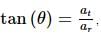 where at is the tangential acceleration and ar is the radial acceleration.
where at is the tangential acceleration and ar is the radial acceleration.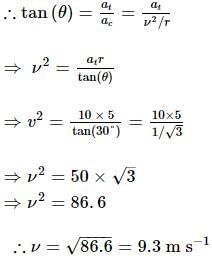


 or if they are subsets of each other, i.e. if A ⊂ B and B ⊂ A, i.e. A = B.
or if they are subsets of each other, i.e. if A ⊂ B and B ⊂ A, i.e. A = B.  R
R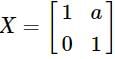 and
and 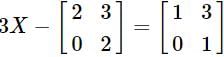 , then a is equal to
, then a is equal to