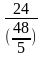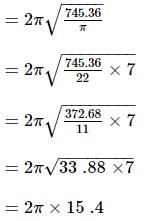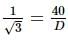SRMJEE Mock Test - 8 (Engineering) - JEE MCQ
30 Questions MCQ Test - SRMJEE Mock Test - 8 (Engineering)
The strength of the magnetic field around a long straight wire carrying current is
A light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
Ice at 0°C is added to 200 g of water initially at 70°C in a vacuum flask. When 50 g of ice is added and completely melts, the temperature of the flask and its contents becomes 40°C. When a further 80 g of ice is added and completely melts, the temperature of the whole system becomes 10°C. Neglecting heat loss to the surroundings, the latent heat of fusion of ice is:
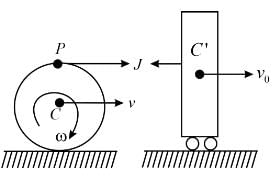
A smooth uniform disc of mass m and radius R is connected with a heavy cart C' by an inextensible string. When the cart is pushed with a velocity v0,
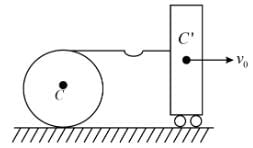
The linear impulse exerted on the disc will be
For a chemical reaction A → B, it is found that the rate of reaction doubles when the concentration of A is increased four times. The order, in terms of A, for this reaction is
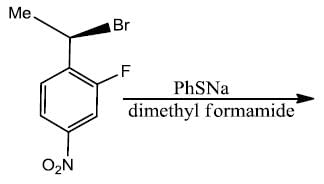
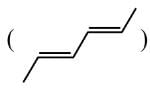
The major product of the following reaction is
The inverse of a symmetric matrix (if it exists) is
If sin A + cos B = a and sin B + cos A = b, then sin (A + B) is equal to
PQ and QR are two focal chords of an ellipse, and the eccentric angles of P, Q, and R are 2α, 2β, and 2γ respectively. Then, the value of tanβtanγ is:
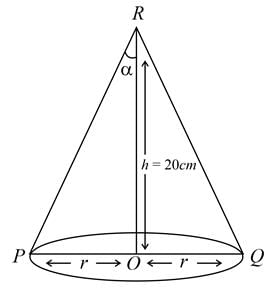
The altitude of a cone is 20 cm and its semi-vertical angle is 30°. If the semi-vertical angle is increasing at the rate of 2° per second, then the radius of the base is increasing at the rate of:
The set of all real numbers x for which log2004(log2003(log2002(log2001x)))) is defined as {x ∣x > c}. The value of c is
ω ≠ 1 s cube root of unity and x + y + z ≠0, then 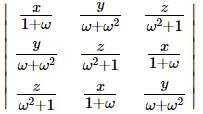 = 0, If
= 0, If
The difference between the age of Guri and Shuri is 4 years. Five years ago, the sum of their ages was 36 years. What will be the ratio of the age of Guri to that of Shuri 7 years from now, if Shuri is younger than Guri?
The pair of equations 15p – 45q = 24 and 6p – 18q = 48/5 has
What would be the circumference of a circle whose area is 745.36 sq. cm?
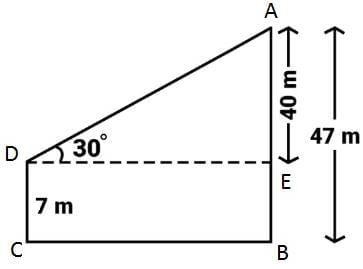
From the top of a platform 7 m high, the angle of elevation of a tower was 30°. If the tower was 47 m high, how far away from the tower was the platform positioned?
In a three-digit number, the digit in the unit’s place is twice the digit in the ten’s place and 1.5 times the digit in the hundred’s place. If the sum of the three digits of the number is 13, what is the number?
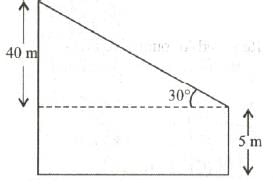
From the top of platform 5 m high, the angle of elevation of a tower was 30°. If the tower is 45 m high, how far away from the tower the platform was positioned?
Directions: In the following question, a phrase/idiom has been given. From the given options, select the most appropriate meaning of the given idiom/phrase.
On the spur of the moment
Which of the following is being referred to as 'certain amount of conflict'?
What method did the Minister suggest to the King to get back the Dog ?
What was the Minister's diagnosis of the Elephant's condition?


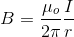

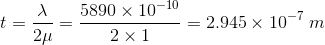
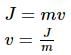
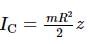
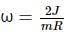
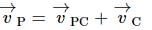
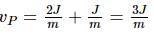
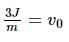
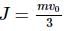

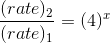
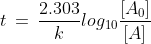


 is
is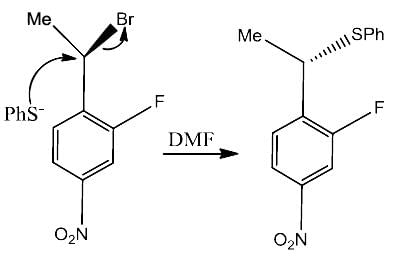

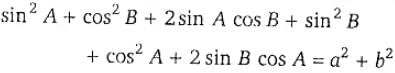

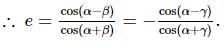
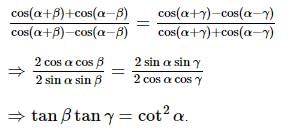
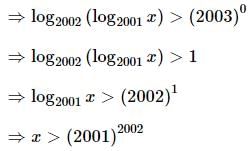
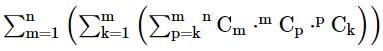 =
= 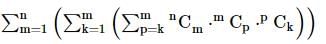
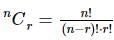
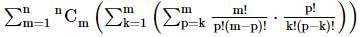
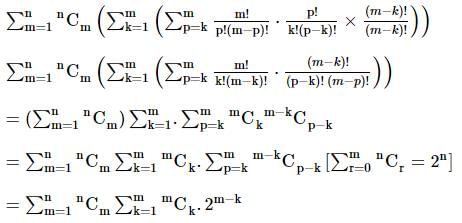
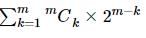
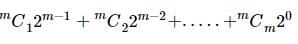
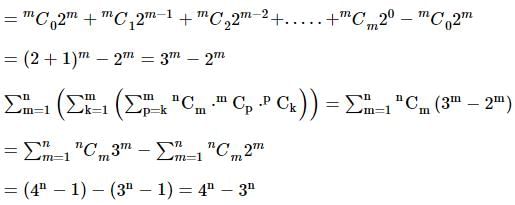

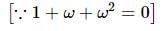
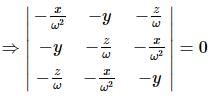
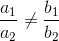
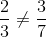

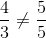
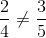
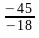 =
=