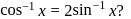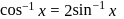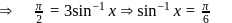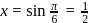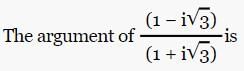SRMJEEE Maths Mock Test - 4 - JEE MCQ
30 Questions MCQ Test - SRMJEEE Maths Mock Test - 4
In a triangle ABC, A = 30o, b = 8, a = 6, then B = sin⁻1 x where x =
The smallest radius of the sphere passing thro'(1,0,0),(0,1,0) and (0,0,1) is
The focus of the parabola given by the equation x² - 2x - 8y - 23 = 0 is
The equation of the sphere concentric with the sphere x2+y2+z2-4x-6y-8z=0 and which passes thro' (0.1,0) is
The differential equation (d2y/dx2)2/3 = (y + (dy/dx))1/2 is of
Given that θ is a acute and that sin θ =3/5. Let x,y be positive real numbers such that 3(x-y) =1, then one set of solutions for x and y expressed in terms of θ is given by
If A and B are two sets such that n(A) = 70, n(B) = 60 and n(A ∪ B)= 110, then n (A ∩ B) is equal to
In a competitions A, B and C are participating. The probability that A wins is twice that of B, the probability that B wins is twice that of C. The probability that A loses is
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is :
a, b, c are three unequal numbers such that a, b, c are in A.P. ; b - a, c - b, a are in G.P., then a : b : c : :


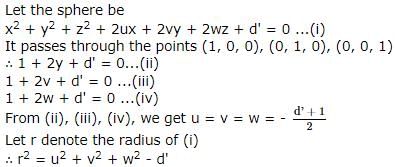
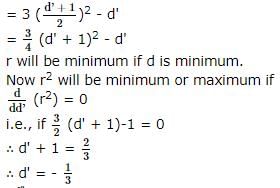
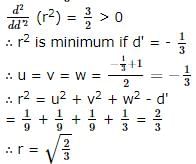

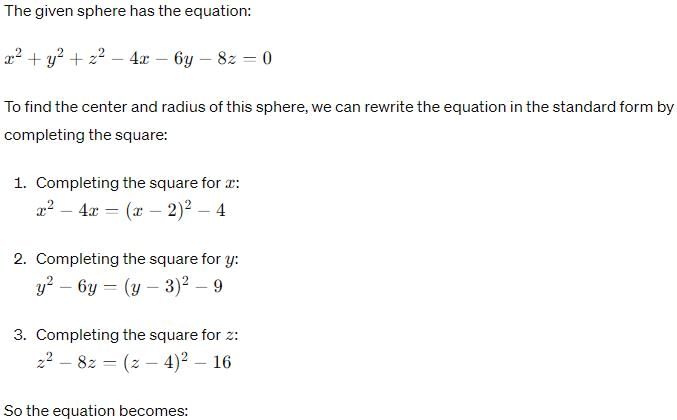


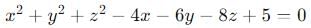
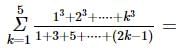
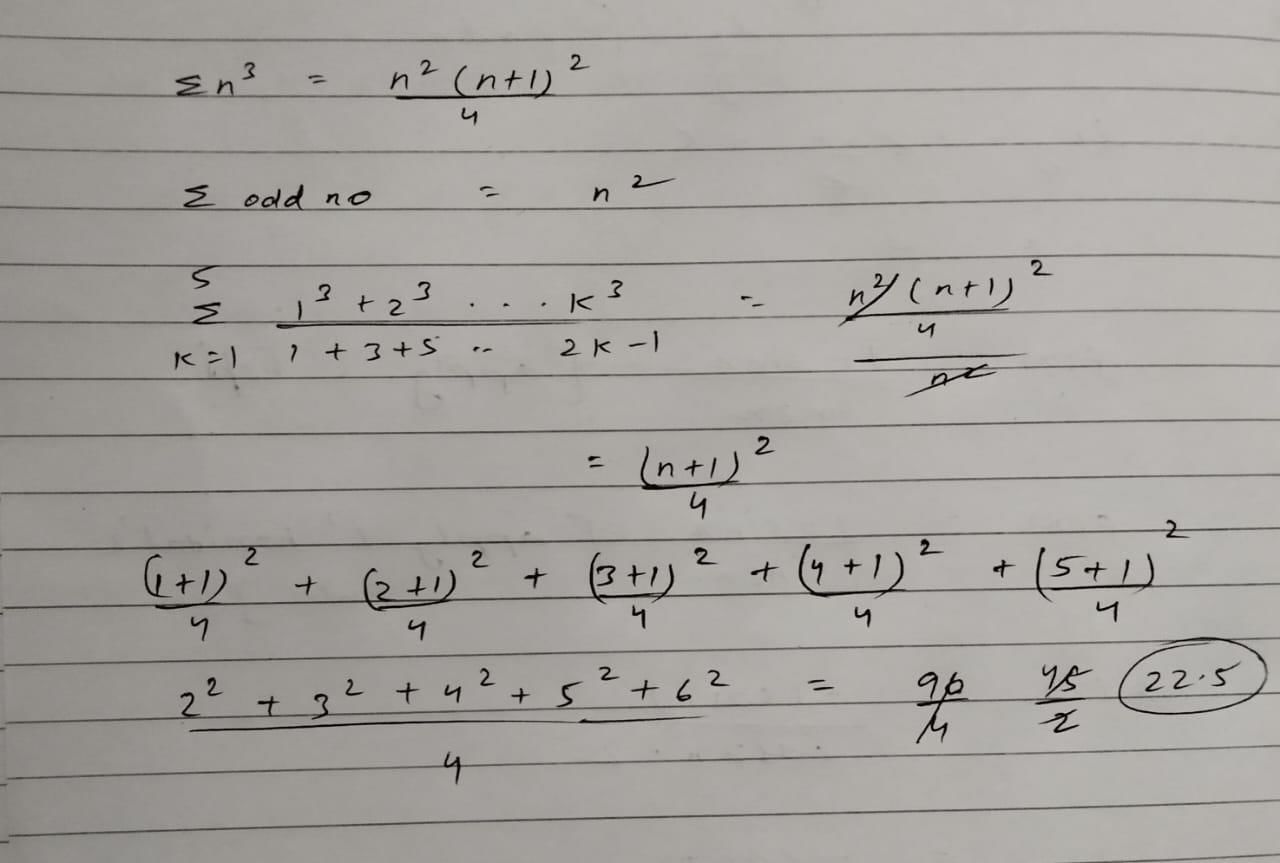
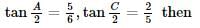
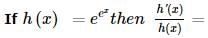
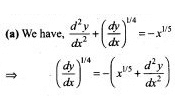
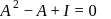 , then
, then 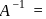
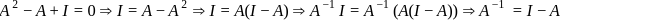

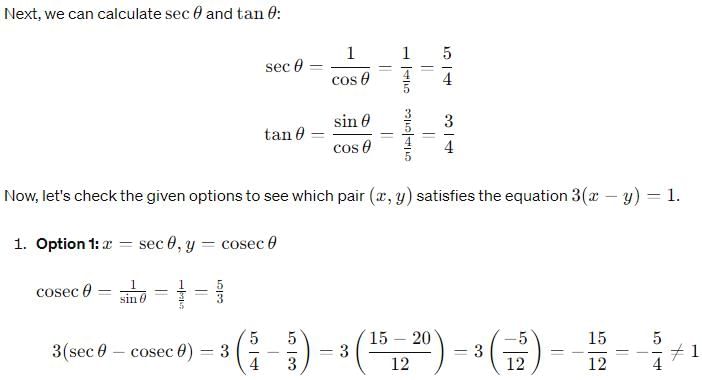
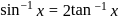 is
is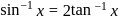
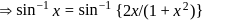
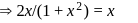


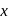 that satisfies the equation
that satisfies the equation