Math Olympiad Test: Coordinate Geometry- 2 - Class 9 MCQ
15 Questions MCQ Test - Math Olympiad Test: Coordinate Geometry- 2
The point of intersection of both the axes is called:
If two points P and Q have same abscissae and different ordinates, then points P and Q will definitely lie on
Minimum distance of point (4, 6) from x -axis will be
If two points M and N lie on y-axis, and have same absolute value of abscissa but different signs. If the abscissa of point M is K, then the distance between M and N is equal to:
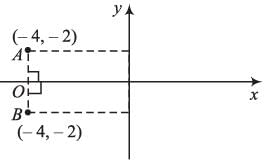
The mirror image of point (-4, -2) about x-axis will lie in:
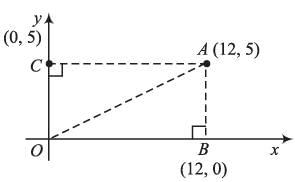
The distance between (12, 5) and origin is
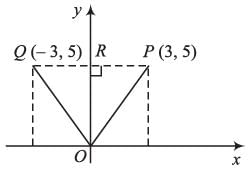
The area of triangle formed by points Q (-3, 5), O (0, 0), P (3, 5) will be (in sq. units)
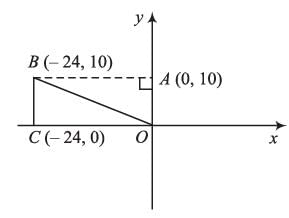
Distance between points (24, 10) and (-48, 10) will be
The difference between ordinates of point P (3, -6) and Q (-6, 3) is
The point of intersection of lines having equations x + y = 6 and x - y = 2, is
Distance of point (- 24 ,10) from origin will be
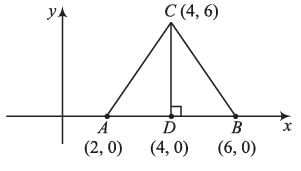
The area of triangle formed by the points A (2, 0), B (6, 0), C (4, 6) is