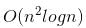Sorting- 1 Free MCQ Practice Test with Solutions - Computer Science Engineering (CSE)

Test: Sorting- 1 - Question 1

What is recurrence for worst case of QuickSort and what is the time complexity in Worst case?

A.
Recurrence is T(n) = T(n-2) + O(n) and time complexity is O(n²)
B.
Recurrence is T(n) = T(n-1) + O(n) and time complexity is O(n²)
C.
Recurrence is T(n) = 2T(n/2) + O(n) and time complexity is O(nLogn)
D.
Recurrence is T(n) = T(n/10) + T(9n/10) + O(n) and time complexity is O(nLogn)

Detailed Solution for Test: Sorting- 1 - Question 1

The worst case of QuickSort occurs when the picked pivot is always one of the corner elements in sorted array. In worst case, QuickSort recursively calls one subproblem with size 0 and other subproblem with size (n-1).
So recurrence is T(n) = T(n-1) + T(0) + O(n).
The above expression can be rewritten as T(n) = T(n-1) + O(n)

void exchange(int *a, int *b)
{
int temp;
temp = *a;
*a = *b;
*b = temp;
}

int partition(int arr[], int si, int ei)
{
int x = arr[ei];
int i = (si - 1);
int j;

for (j = si; j <= ei - 1; j++)
{
   if(arr[j] <= x)
   {
   i++;
   exchange(&arr[i], &arr[j]);
   }
}

exchange (&arr[i + 1], &arr[ei]);
return (i + 1);
}

/* Implementation of Quick Sort
arr[] --> Array to be sorted
si --> Starting index
ei --> Ending index
*/
void quickSort(int arr[], int si, int ei)
{
int pi; /* Partitioning index */
if(si < ei)
{
   pi = partition(arr, si, ei);
   quickSort(arr, si, pi - 1);
   quickSort(arr, pi + 1, ei);
}
}

Test: Sorting- 1 - Question 2

Suppose we have a O(n) time algorithm that finds median of an unsorted array. Now consider a QuickSort implementation where we first find median using the above algorithm, then use median as pivot. What will be the worst case time complexity of this modified QuickSort.

A.
O(n² Logn)
B.
O(n Logn)
C.
O(n Logn Logn)
D.
none

Detailed Solution for Test: Sorting- 1 - Question 2

1. Finding the Median:

The algorithm uses a method to find the median in linear time, which is O(n).
This median is used as the pivot in QuickSort.
Using the median ensures that the array is split into two nearly equal halves, which avoids the worst-case unbalanced splits of standard QuickSort.

2. Partitioning:

Partitioning the array around the median also takes O(n) time.

3. Recursive Calls:

Since the array is split into two equal (or nearly equal) parts, the recurrence relation for the time complexity becomes:

T(n) = 2T(n/2) + O(n) + O(n)
The first O(n) is for finding the median, and the second O(n) is for partitioning the array.
This simplifies to:

T(n) = 2T(n/2) + O(n)

4. Solving the Recurrence:

This recurrence relation is similar to the one used in MergeSort.
Its solution is O(n log n).

Final Answer:

B: O(n log n)

So, the worst-case time complexity of this modified QuickSort (that uses the median as pivot) is O(n log n).

Test: Sorting- 1 - Question 3

Which of the following sorting algorithms in its typical implementation gives best performance when applied on an array which is sorted or almost sorted (maximum 1 or two elements are misplaced).

A.
Quick Sort
B.
Heap Sort
C.
Merge Sort
D.
Insertion Sort

Detailed Solution for Test: Sorting- 1 - Question 3

Insertion sort takes linear time when input array is sorted or almost sorted (maximum 1 or 2 elements are misplaced). All other sorting algorithms mentioned above will take more than linear time in their typical implementation.

Test: Sorting- 1 - Question 4

Suppose we are sorting an array of eight integers using quicksort, and we have just finished the first partitioning with the array looking like this: 2 5 1 7 9 12 11 10 Which statement is correct?

A.
The pivot could be either the 7 or the 9.
B.
The pivot could be the 7, but it is not the 9
C.
The pivot is not the 7, but it could be the 9
D.
Neither the 7 nor the 9 is the pivot.

Detailed Solution for Test: Sorting- 1 - Question 4

7 and 9 both are at their correct positions (as in a sorted array). Also, all elements on left of 7 and 9 are smaller than 7 and 9 respectively and on right are greater than 7 and 9 respectively.

Test: Sorting- 1 - Question 5

Consider a situation where swap operation is very costly. Which of the following sorting algorithms should be preferred so that the number of swap operations are minimized in general?

A.
Heap Sort
B.
Selection Sort
C.
Insertion Sort
D.
Merge Sort

Detailed Solution for Test: Sorting- 1 - Question 5

Selection sort makes O(n) swaps which is minimum among all sorting algorithms mentioned above.

Test: Sorting- 1 - Question 6

Suppose we are sorting an array of eight integers using heapsort, and we have just finished some heapify (either maxheapify or minheapify) operations. The array now looks like this: 16 14 15 10 12 27 28. How many heapify operations have been performed on root of heap?

A.
1
B.
2
C.
3 or 4
D.
5 or 6

Detailed Solution for Test: Sorting- 1 - Question 6

In Heapsort, we first build a heap, then we do following operations till the heap size becomes 1. a) Swap the root with last element b) Call heapify for root c) reduce the heap size by 1. In this question, it is given that heapify has been called few times and we see that last two elements in given array are the 2 maximum elements in array. So situation is clear, it is maxheapify whic has been called 2 times.

Test: Sorting- 1 - Question 7

What is the best time complexity of bubble sort?

A.
N²
B.
N logN
C.
N
D.
N(logN)²

Detailed Solution for Test: Sorting- 1 - Question 7

The only significant advantage that bubble sort has over most other algorithms, even quicksort, but not insertion sort, is that the ability to detect that the list is sorted efficiently is built into the algorithm. When the list is already sorted (best-case), the complexity of bubble sort is only O(n).

Test: Sorting- 1 - Question 8

You have to sort 1 GB of data with only 100 MB of available main memory. Which sorting technique will be most appropriate?

A.
Heap sort
B.
Merge sort
C.
Quick sort
D.
Insertion sort

Detailed Solution for Test: Sorting- 1 - Question 8

The data can be sorted using external sorting which uses merging technique. This can be done as follows: 1. Divide the data into 10 groups each of size 100. 2. Sort each group and write them to disk. 3. Load 10 items from each group into main memory. 4. Output the smallest item from the main memory to disk. Load the next item from the group whose item was chosen. 5. Loop step #4 until all items are not outputted. The step 3-5 is called as merging technique.

Test: Sorting- 1 - Question 9

Given an unsorted array. The array has this property that every element in array is at most k distance from its position in sorted array where k is a positive integer smaller than size of array. Which sorting algorithm can be easily modified for sorting this array and what is the obtainable time complexity?

A.
Insertion Sort with time complexity O(kn).
B.
Heap Sort with time complexity O(nLogk).
C.
Quick Sort with time complexity O(kLogk).
D.
Merge Sort with time complexity O(kLogk).

Detailed Solution for Test: Sorting- 1 - Question 9

To sort the array firstly create a min-heap with first k+1 elements and a separate array as resultant array.
Because elements are at most k distance apart from original position so, it is guranteed that the smallest element will be in this K+1 elements.
Remove the smallest element from the min-heap(extract min) and put it in the result array.
Now,insert another element from the unsorted array into the mean-heap, now,the second smallest element will be in this, perform extract min and continue this process until no more elements are in the unsorted array.finally, use simple heap sort for the remaining elements

Time Complexity

O(k) to build the initial min-heap.
O((n-k)logk) for remaining elements.
0(1) for extract min.

So overall O(k) + O((n-k)logk) + 0(1) = O(nlogk)

Test: Sorting- 1 - Question 10

Which of the following is not a stable sorting algorithm in its typical implementation.

A.
Insertion Sort
B.
Merge Sort
C.
Quick Sort
D.
Bubble Sort

Detailed Solution for Test: Sorting- 1 - Question 10

Out of the given options quick sort is the only algorithm which is not stable. Merge sort is a stable sorting algorithm.

Test: Sorting- 1 - Question 11

Which of the following is not true about comparison based sorting algorithms?

A.
The minimum possible time complexity of a comparison based sorting algorithm is O(nLogn) for a random input array
B.
Any comparison based sorting algorithm can be made stable by using position as a criteria when two elements are compared
C.
Counting Sort is not a comparison based sorting algorithm
D.
Heap Sort is not a comparison based sorting algorithm

Detailed Solution for Test: Sorting- 1 - Question 11

Any comparison based sorting algorithm can be made stable by using position as a criteria when two elements are compared. Counting Sort is not a comparison based sorting algorithm. Heap Sort is not a comparison based sorting algorithm.

Test: Sorting- 1 - Question 12

What is the worst case time complexity of insertion sort where position of the data to be inserted is calculated using binary search?

A.
N
B.
NlogN
C.
N²
D.
N(logN)²

Detailed Solution for Test: Sorting- 1 - Question 12

Applying binary search to calculate the position of the data to be inserted doesn't reduce the time complexity of insertion sort. This is because insertion of a data at an appropriate position involves two steps: 1. Calculate the position. 2. Shift the data from the position calculated in step #1 one step right to create a gap where the data will be inserted. Using binary search reduces the time complexity in step #1 from O(N) to O(logN). But, the time complexity in step #2 still remains O(N). So, overall complexity remains O(N²).

Test: Sorting- 1 - Question 13

The tightest lower bound on the number of comparisons, in the worst case, for comparison-based sorting is of the order of

A.
N
B.
N²
C.
NlogN
D.
N(logN)²

Detailed Solution for Test: Sorting- 1 - Question 13

The number of comparisons that a comparison sort algorithm requires increases in proportion to Nlog(N), where N is the number of elements to sort. This bound is asymptotically tight: Given a list of distinct numbers (we can assume this because this is a worst-case analysis), there are N factorial permutations exactly one of which is the list in sorted order. The sort algorithm must gain enough information from the comparisons to identify the correct permutations. If the algorithm always completes after at most f(N) steps, it cannot distinguish more than 2^f(N) cases because the keys are distinct and each comparison has only two possible outcomes. Therefore, 2^f(N) >= N! or equivalently f(N) >= log(N!). Since log(N!) is Omega(NlogN), the answer is NlogN. For more details, read here

Test: Sorting- 1 - Question 14

In a modified merge sort, the input array is splitted at a position one-third of the length(N) of the array. What is the worst case time complexity of this merge sort?

A.
N(logN base 3)
B.
N(logN base 2/3)
C.
N(logN base 1/3)
D.
N(logN base 3/2)

Detailed Solution for Test: Sorting- 1 - Question 14

The time complexity is given by: T(N) = T(N/3) + T(2N/3) + N Solving the above recurrence relation gives, T(N) = N(logN base 3/2)

Test: Sorting- 1 - Question 15

Which sorting algorithm will take least time when all elements of input array are identical? Consider typical implementations of sorting algorithms.

A.
Insertion Sort
B.
Heap Sort
C.
Merge Sort
D.
Selection Sort

Detailed Solution for Test: Sorting- 1 - Question 15

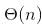The insertion sort will take time when input array is already sorted.

Test: Sorting- 1 - Question 16

A list of n string, each of length n, is sorted into lexicographic order using the merge-sort algorithm. The worst case running time of this computation is

A.
B.
C.
D.
O(n²)

Detailed Solution for Test: Sorting- 1 - Question 16

The recurrence tree for merge sort will have height Log(n). And O(n²) work will be done at each level of the recurrence tree (Each level involves n comparisons and a comparison takes O(n) time in worst case). So time complexity of this Merge Sort will be

Test: Sorting- 1 - Question 17

In quick sort, for sorting n elements, the (n/4)th smallest element is selected as pivot using an O(n) time algorithm. What is the worst case time complexity of the quick sort?

A.
θ(n)
B.
θ(nLogn)
C.
θ(n²)
D.
θ(n² log n)

Detailed Solution for Test: Sorting- 1 - Question 17

The recursion expression becomes: T(n) = T(n/4) + T(3n/4) + cn After solving the above recursion, we get θ(nLogn)

Test: Sorting- 1 - Question 18

Consider the Quicksort algorithm. Suppose there is a procedure for finding a pivot element which splits the list into two sub-lists each of which contains at least one-fifth of the elements. Let T(n) be the number of comparisons required to sort n elements. Then

A.
T(n) <= 2T(n/5) + n
B.
T(n) <= T(n/5) + T(4n/5) + n
C.
T(n) <= 2T(4n/5) + n
D.
T(n) <= 2T(n/2) + n

Detailed Solution for Test: Sorting- 1 - Question 18

For the case where n/5 elements are in one subset, T(n/5) comparisons are needed for the first subset with n/5 elements, T(4n/5) is for the rest 4n/5 elements, and n is for finding the pivot. If there are more than n/5 elements in one set then other set will have less than 4n/5 elements and time complexity will be less than T(n/5) + T(4n/5) + n because recursion tree will be more balanced.

Test: Sorting- 1 - Question 19

Which of the following sorting algorithms has the lowest worst-case complexity?

A.
Merge Sort
B.
Bubble Sort
C.
Quick Sort
D.
Selection Sort

Detailed Solution for Test: Sorting- 1 - Question 19

Worst case complexities for the above sorting algorithms are as follows: Merge Sort — nLogn Bubble Sort — n² Quick Sort — n² Selection Sort — n²

Test: Sorting- 1 - Question 20

Which sorting algorithms is most efficient to sort string consisting of ASCII characters?

A.
Quick sort
B.
Heap sort
C.
Merge sort
D.
Counting sort

Detailed Solution for Test: Sorting- 1 - Question 20

Counting sort algorithm is efficient when range of data to be sorted is fixed. In the above question, the range is from 0 to 255(ASCII range). Counting sort uses an extra constant space proportional to range of data.

Test: Sorting- 1 - Computer Science Engineering (CSE) MCQ

20 Questions MCQ Test - Test: Sorting- 1

What is recurrence for worst case of QuickSort and what is the time complexity in Worst case?

Suppose we have a O(n) time algorithm that finds median of an unsorted array. Now consider a QuickSort implementation where we first find median using the above algorithm, then use median as pivot. What will be the worst case time complexity of this modified QuickSort.

1. Finding the Median:

2. Partitioning:

3. Recursive Calls:

4. Solving the Recurrence:

Final Answer:

Which of the following sorting algorithms in its typical implementation gives best performance when applied on an array which is sorted or almost sorted (maximum 1 or two elements are misplaced).

Top Courses for Computer Science Engineering (CSE)

Schools

Competitive Examinations

Quick Access Links

Technical Exams

Important Questions for Sorting- 1

Sorting- 1 MCQs with Answers

Online Tests for Sorting- 1