Test: Combinatory- 3 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Combinatory- 3
How many onto (or surjective) functions are there from an n-element (n >= 2) set to a 2-element set?
What is the possible number of reflexive relations on a set of 5 elements?
What is the maximum number of different Boolean functions involving n Boolean variables?
Suppose that a robot is placed on the Cartesian plane. At each step it is allowed to move either one unit up or one unit right, i.e., if it is at (i,j) then it can move to either (i+1,j) or (i,j+1). How many distinct paths are there for the robot to reach the point (10,10) starting from the initial position (0, 0)
Consider the data given in above question. Suppose that the robot is not allowed to traverse the line segment from (4,4) to (5,4). With this constraint, how many distinct paths are there for the robot to reach (10,10) starting from (0,0)?
Let ∑ be a finite non-empty alphabet and let 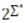 be the power set of ∑*. Which one of the following is TRUE?
be the power set of ∑*. Which one of the following is TRUE?
The number of different n × n symmetric matrices with each element being either 0 or 1 is: (Note: power(2, x) is same as 2x)
Mala has a colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour-pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement ?
Let A be a sequence of 8 distinct integers sorted in ascending order. How many distinct pairs of sequences, B and C are there such that
(i) each is sorted in ascending order,
(ii) B has 5 and C has 3 elements, and
(iii) the result of merging B and C gives A?
n couples are invited to a party with the condition that every husband should be accompanied by his wife. However, a wife need not be accompanied by her husband. The number of different gatherings possible at the party is
m identical balls are to be placed in n distinct bags. You are given that m ≥ kn, where, k is a natural number ≥ 1. In how many ways can the balls be placed in the bags if each bag must contain at least k balls?
For a set A, the power set of A is denoted by 2A. If A = {5, {6}, {7}}, which of the following options are True.
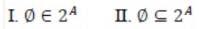

The number of 4 digit numbers having their digits in non-decreasing order (from left to right) constructed by using the digits belonging to the set {1, 2, 3} is ____.
How many substrings of different length (non-zero) can be formed from a character string of length n ?
|
55 docs|215 tests
|
|
55 docs|215 tests
|




















