Test: Graphs Theory- 2 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Graphs Theory- 2
If G is a forest with n vertices and k connected components, how many edges does G have?
Let d denote the minimum degree of a vertex in a graph. For all planar graphs on n vertices with d ≥ 3, which one of the following is TRUE?
The 2n vertices of a graph G corresponds to all subsets of a set of size n, for n >= 6 . Two vertices of G are adjacent if and only if the corresponding sets intersect in exactly two elements. The number of vertices of degree zero in G is:
The 2n vertices of a graph G corresponds to all subsets of a set of size n, for n >= 6. Two vertices of G are adjacent if and only if the corresponding sets intersect in exactly two elements. The number of connected components in G is:
Let G be a simple connected planar graph with 13 vertices and 19 edges. Then, the number of faces in the planar embedding of the graph is
Let G be a simple graph with 20 vertices and 100 edges. The size of the minimum vertex cover of G is 8. Then, the size of the maximum independent set of G is
Let s and t be two vertices in a undirected graph G + (V, E) having distinct positive edge weights. Let [X, Y] be a partition of V such that s ∈ X and t ∈ Y. Consider the edge e having the minimum weight amongst all those edges that have one vertex in X and one vertex in Y. Let the weight of an edge e denote the congestion on that edge. The congestion on a path is defined to be the maximum of the congestions on the edges of the path. We wish to find the path from s to t having minimum congestion. Which one of the following paths is always such a path of minimum congestion?
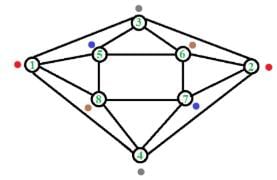
The minimum number of colours required to colour the following graph, such that no two adjacent vertices are assigned the same colour, is
Let G be an arbitrary graph with n nodes and k components. If a vertex is removed from G, the number of components in the resultant graph must necessarily lie between
How many perfect matchings are there in a complete graph of 6 vertices ?
A graph G = (V, E) satisfies |E| ≤ 3 |V| - 6. The min-degree of G is defined as
Therefore, min-degree of G cannot be
The minimum number of colours required to colour the vertices of a cycle with η nodes in such a way that no two adjacent nodes have the same colour is
Maximum number of edges in a n - node undirected graph without self loops is
Let G be a connected planar graph with 10 vertices. If the number of edges on each face is three, then the number of edges in G is _______________.
A graph is self-complementary if it is isomorphic to its complement. For all self-complementary graphs on n vertices, n is
In a connected graph, a bridge is an edge whose removal disconnects a graph. Which one of the following statements is True?
What is the number of vertices in an undirected connected graph with 27 edges, 6 vertices of degree 2, 3 vertices of degree 4 and remaining of degree 3?
The minimum number of colours that is sufficient to vertex-colour any planar graph is _______________
[This Question was originally a Fill-in-the-blanks Question]
If all the edge weights of an undirected graph are positive, then any subset of edges that connects all the vertices and has minimum total weight is a
|
55 docs|215 tests
|
|
55 docs|215 tests
|