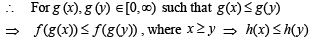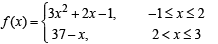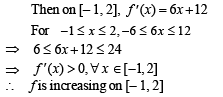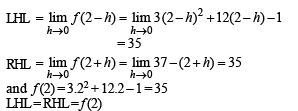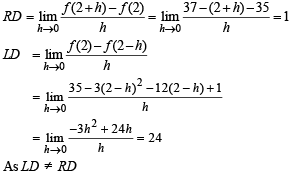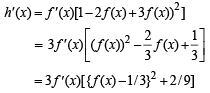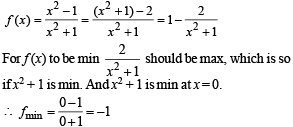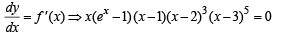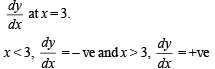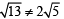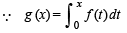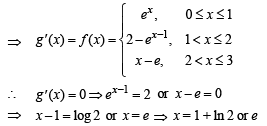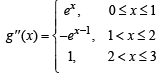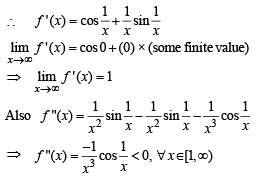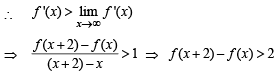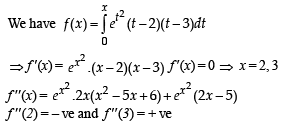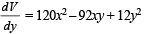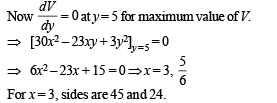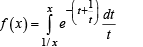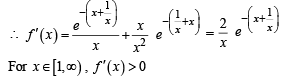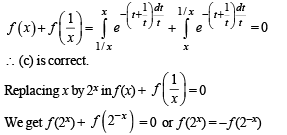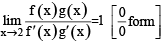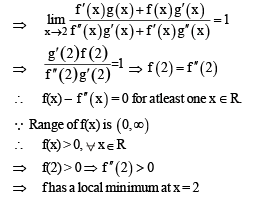Multiple Correct MCQ Of Applications Of Derivatives, Past Year Questions JEE Advance, Class 12, Maths - JEE MCQ
17 Questions MCQ Test - Multiple Correct MCQ Of Applications Of Derivatives, Past Year Questions JEE Advance, Class 12, Maths
Let P(x) = a0 + a1x2 + a2x4 + ...... + anx2n be a polynomial in a real variable x with 0 < a0 < a1 < a2 < ..... < an. . The function P(x) has
If the line ax + by + c = 0 is a normal to the curve xy = 1, then
The smallest positive root of the equation, tan x – x = 0 lies in
Let f and g be in creasin g and decreasing function s, respectively from [0, ∞) to [0, ∞). Let h(x) = f (g(x)). If h(0) = 0, then h(x) – h (1) is
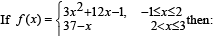
Let h(x) = f(x) – (f(x))2 + (f(x))3 for every real number x. Then
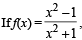 for every real number x, then the minimum value of f
for every real number x, then the minimum value of f
The number of values of x where the function f(x) = cos x + cos (√2 x) attains its maximum is
The function  dt has a local minimum at x =
dt has a local minimum at x =
f(x) is cubic polynomial with f(2) = 18 and f(1) = –1. Also f(x) has local maxima at x = –1 and f '(x) has local minima at x = 0, then
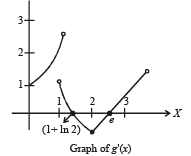
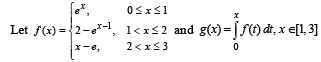 then g(x) has
then g(x) has
For the function
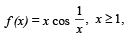
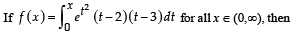
A rectangular sheet of fixed perimeter with sides having their lengths in the ratio 8 : 15 is converted into an open rectangular box by folding after removing squares of equal area from all four corners. If the total area of removed squares is 100, the resulting box has maximum volume.
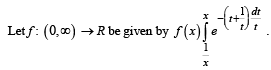 Then
Then
 be continuous functions which are twice differentiable on the interval (–1, 2). Let the values of f and g at the points –1, 0 and 2 be as given in the following table:
be continuous functions which are twice differentiable on the interval (–1, 2). Let the values of f and g at the points –1, 0 and 2 be as given in the following table:

In each of the intervals (–1, 0) and (0, 2) the function (f – 3g)" never vanishes. Then the correct statement(s) is(are)
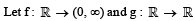 be twice differen tiable functions such that f" and g" are continuous functions on
be twice differen tiable functions such that f" and g" are continuous functions on 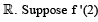 = g(2)= 0, f"(2) ≠ 0 and g'(2) ≠ 0. If
= g(2)= 0, f"(2) ≠ 0 and g'(2) ≠ 0. If 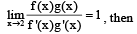


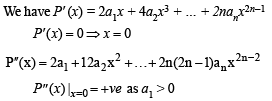
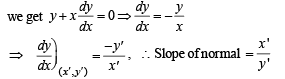
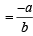
 … (2)
… (2)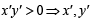 are of same sign
are of same sign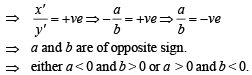

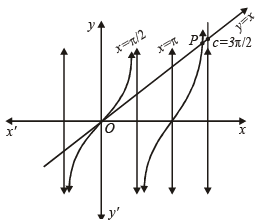
 ........ (1)
........ (1)