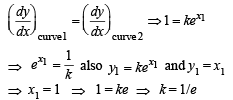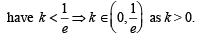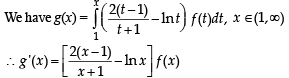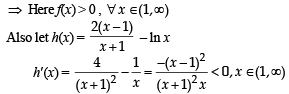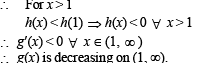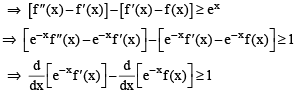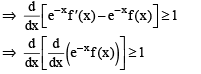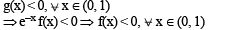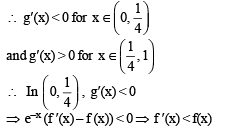Test: Comprehension Based Questions: Applications of Derivatives - JEE MCQ
7 Questions MCQ Test - Test: Comprehension Based Questions: Applications of Derivatives
PASSAGE - 1
If a continuous function f defined on the real line R, assumes positive and negative values in R then the equation f(x) = 0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum value is negative then the equation f(x) = 0 has a root in R.
Consider f(x) = kex – x for all real x where k is a real constant.
Q. The line y = x meets y = kex for k < 0 at
PASSAGE - 1
If a continuous function f defined on the real line R, assumes positive and negative values in R then the equation f(x) = 0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum value is negative then the equation f(x) = 0 has a root in R.
Consider f(x) = kex – x for all real x where k is a real constant.
Q. The positive value of k for which kex – x = 0 has only one root is
PASSAGE - 1
If a continuous function f defined on the real line R, assumes positive and negative values in R then the equation f(x) = 0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum value is negative then the equation f(x) = 0 has a root in R.
Consider f(x) = kex – x for all real x where k is a real constant.
Q. For k > 0, the set of all values of k for which kex – x = 0 has two distinct roots is
PASSAGE - 2
Let f (x) = (1 – x)2 sin2x + x2 for all x ∈ I R and let 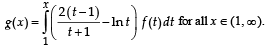
Q.
Consider the statements:
P : Th er e exists some x ∈ R such th at f (x) + 2 x = 2(1 + x2)
Q : There exists some x ∈ R such that 2 f (x) + 1 = 2x (1 + x) Then
PASSAGE - 2
Let f (x) = (1 – x)2 sin2x + x2 for all x ∈ I R and let 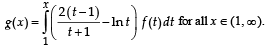
Q. Which of the following is true?
PASSAGE - 3
 (the set of all real numbers) be a function. Suppose the function f is twice differentiable, f(0) = f(1) = 0 and satisfies
(the set of all real numbers) be a function. Suppose the function f is twice differentiable, f(0) = f(1) = 0 and satisfies 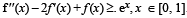
Q. Which of the following is true for 0 < x < 1?
PASSAGE - 3
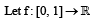 (the set of all real numbers) be a function. Suppose the function f is twice differentiable, f(0) = f(1) = 0 and satisfies
(the set of all real numbers) be a function. Suppose the function f is twice differentiable, f(0) = f(1) = 0 and satisfies 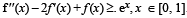
Q. If the function e–x f(x) assumes its minimum in the interval  which of the following is true?
which of the following is true?