Test: MCQs (One or More Correct Option): Circle | JEE Advanced - JEE MCQ
6 Questions MCQ Test - Test: MCQs (One or More Correct Option): Circle | JEE Advanced
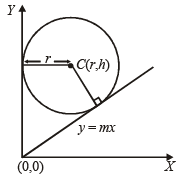
The equations of the tangents drawn from the origin to the circle x2 + y2 – 2rx – 2hy + h2 = 0, are (1988 - 2 Marks)
The number of common tangents to the circles x2 + y2 = 4 and x2 + y2 – 6x – 8y = 24 is (1998 - 2 Marks)
If the circle x2 + y2 = a2 intersects the hyperbola xy = c2 in four points P(x1, y1), Q(x2, y2), R(x3, y3), S(x4, y4), then (1998 - 2 Marks)
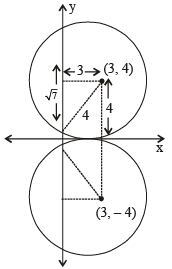
Circle(s) touching x-axis at a distance 3 from the origin and having an intercept of length 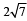 on y-axis is (are) (JEE Adv. 2013)
on y-axis is (are) (JEE Adv. 2013)
A circle S passes through the point (0, 1) and is orthogonal to the circles (x – 1)2 + y2 = 16 and x2 + y2 = 1. Then (JEE Adv. 2014)
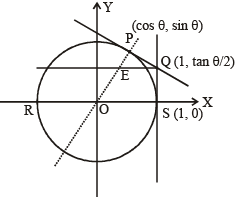
Let RS be the diameter of the circle x2 + y2 = 1, where S is the point (1, 0). Let P be a variable point (other than R and S) on the circle and tangents to the circle at S and P meet at the point Q. The normal to the circle at P intersects a line drawn through Q parallel to RS at point E. Then the locus of E passes through the point(s) (JEE Adv. 2016)


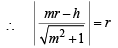
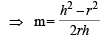


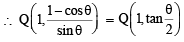
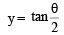
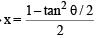
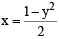 or y2 = 1 – 2x
or y2 = 1 – 2x and
and