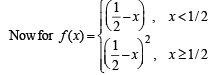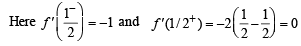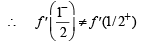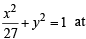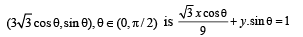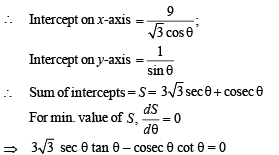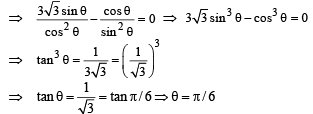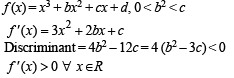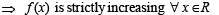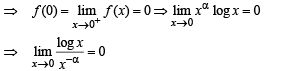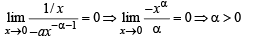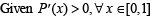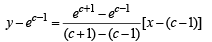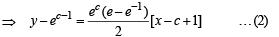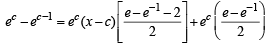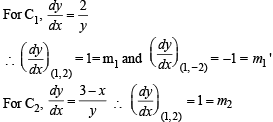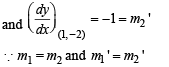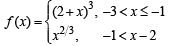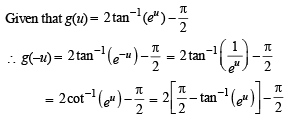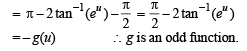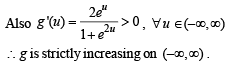Test: Single Correct MCQs: Applications of Derivatives | JEE Advanced - Year 11 MCQ
30 Questions MCQ Test - Test: Single Correct MCQs: Applications of Derivatives | JEE Advanced
If a + b + c = 0, then the quadratic equation 3ax2 + 2bx + c = 0 h as
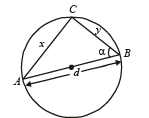
AB is a diameter of a circle and C is any point on the circumference of the circle. Then
The normal to the curve x = a (cos θ + θ sin θ), y = a (sin θ – θ cos θ) at any point ‘θ’ is such that
If y = a ln x + bx2 + x has its extremum values at x = –1 and x = 2, then
Which one of the following curves cut the parabola y2 = 4ax at right angles?
Th e fun ction defined by f(x) = (x + 2) e–x is
The function 
On the interval [0, 1] the function x25 (1 - x)75 takes its maximum value at the point
The slope of the tangent to a curve y = f(x) at [x, f(x)] is 2x + 1. If the curve passes through the point (1, 2), then the area bounded by the curve, the x-axis and the line x = 1 is
 then in this interval
then in this interval
The function f(x) = sin4 x + cos4 x increases if
Consider the following statments in S and R
S : Both sin x and cos x are decreasing functions in the 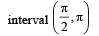
R: If a differentiable function decreases in an interval (a, b), then its derivative also decreases in (a, b).
Which of the following is true ?
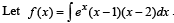 Then f decreases in the interval
Then f decreases in the interval
If the normal to the curve y = f(x) at the point (3,4) makes an angle 3π/4 with the positive x-axis, then f '(3) =
For all x ∈ (0,1)
If f (x) = xe x (1-x) , then f (x) is
The triangle formed by the tangent to the curve f(x) = x2 + bx - b at the point (1, 1) and the coordinate axes, lies in the first quadrant. If its area is 2, then the value of b is
Let f(x) = (1 + b2)x2 + 2bx + 1 and let m(b) be the minimum value of f(x). As b varies, the range of m(b) is
The length of a longest interval in which the function 3 sin x – 4 sin3x is increasing, is
The point(s) on the curve y3 + 3x2 = 12y where the tangent is vertical, is (are)
In [0,1] Lagranges Mean Value theorem is NOT applicable to
Tangent is drawn to ellipse
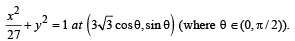
Then the value of θ such that sum of intercepts on axes made by this tangent is minimum, is
If f (x) = x3 + bx2 + cx + d and 0 < b2 < c, then in (–∞, ∞)
If f (x) = xα log x and f (0) = 0, then the value of α for which Rolle’s theorem can be applied in [0, 1] is
If P(x) is a polynomial of degree less than or equal to 2 and S is the set of all such polynomials so that P(0) = 0,
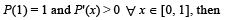
The tangent to the curve y = ex drawn at the point (c, ec) intersects the line joining the points (c – 1, ec–1) and (c + 1, ec + 1)
Consider the two curves C1 : y2 = 4x, C2 : x2 + y2 – 6x + 1 = 0.
Then,
The total number of local maxima and local minima of the function 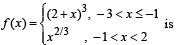
Let the function 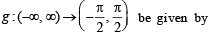 be given by
be given by 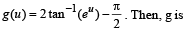


 such that 2
such that 2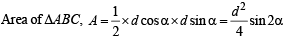

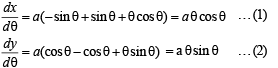
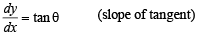
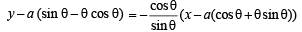
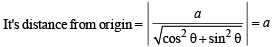
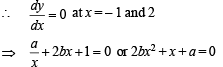
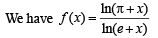
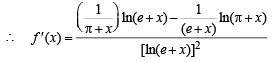

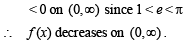
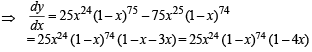
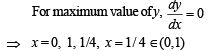
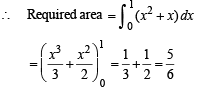
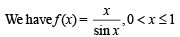

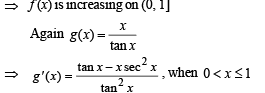
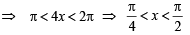
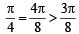
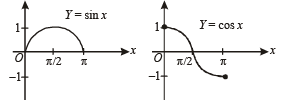
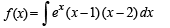
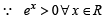
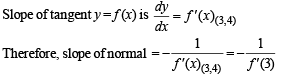
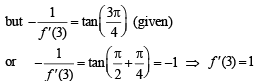

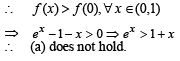
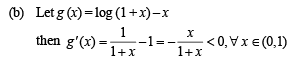
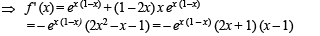
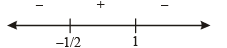
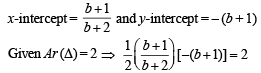
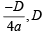 being the discreminant.
being the discreminant.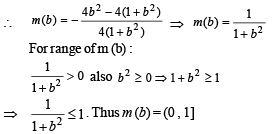
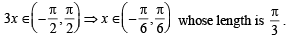
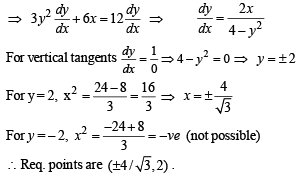
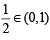 for the rest of the parts critical point 0 ∉ (0, 1). It can be easily seen that functions in options (b), (c) and (d) are continuous on [0, 1] and differentiable in (0, 1).
for the rest of the parts critical point 0 ∉ (0, 1). It can be easily seen that functions in options (b), (c) and (d) are continuous on [0, 1] and differentiable in (0, 1).