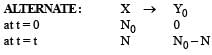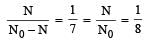31 Year NEET Previous Year Questions: Nuclei - NEET MCQ
30 Questions MCQ Test Physics Class 12 - 31 Year NEET Previous Year Questions: Nuclei
In the reaction , 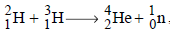 if the binding energies of
if the binding energies of 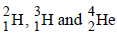 are respectively, a, b and c (in MeV), then the energy (in MeV) released in this reaction is [2005]
are respectively, a, b and c (in MeV), then the energy (in MeV) released in this reaction is [2005]
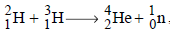 if the binding energies of
if the binding energies of 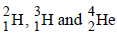 are respectively, a, b and c (in MeV), then the energy (in MeV) released in this reaction is [2005]
are respectively, a, b and c (in MeV), then the energy (in MeV) released in this reaction is [2005]In any fission process, the ratio 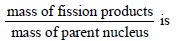 [2005]
[2005]
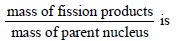 [2005]
[2005]Fission of nuclei is possible because thebinding energy per nucleon in them [2005]
The binding energy of deuteron is 2.2 MeV and that of  is 28 MeV. If two deuterons are fused to form one
is 28 MeV. If two deuterons are fused to form one  then the energy released is [2006]
then the energy released is [2006]
In a radioactive material the activity at time t1 is R1 and at a later time t2, it is R2. If the decay constant of the material is λ, then [2006]
Two radioactive substances A and B have decay constants 5λ and λ respectively. At t = 0 they have the same number of nuclei. The ratio of number of nuclei of A to those of B will be (1/e)2 after a time interval [2007]
In a radioactive decay process, the negativelycharged emitted β -particles are [2007]
A nucleus AZX has mass represented by M (A, Z). If Mp and Mn denote the mass of proton and neutron respectively and B.E. the binding energy in MeV, then [2007]
If the nucleus 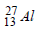 has nuclear radius of about 3.6 fm, then
has nuclear radius of about 3.6 fm, then 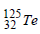 would have its radius approximately as [2007]
would have its radius approximately as [2007]
Two radioactive materials X1 and X2 have decay constants 5λ and λ respectively. If initially they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will be 1/e after a time
If M (A; Z), Mp and Mn denote the masses of the nucleus 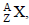 proton and neutron respectively in units of u ( 1u = 931.5 MeV/c2) and BE represents its bonding energy in MeV, then [2008]
proton and neutron respectively in units of u ( 1u = 931.5 MeV/c2) and BE represents its bonding energy in MeV, then [2008]
Two nuclei have their mass numbers in the ratioof 1 : 3. The ratio of their nuclear densities wouldbe [2008]
In the nuclear decay given below: [2009]
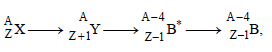 the particles emitted in the sequence are
the particles emitted in the sequence are
The mass of a 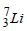 nucleus is 0.042 u less than the sum of the masses of all its nucleons. The binding energy per nucleon of
nucleus is 0.042 u less than the sum of the masses of all its nucleons. The binding energy per nucleon of 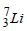 nucleus is nearly
nucleus is nearly
The activity of a radioactive sample is measured as N0 counts per minute at t = 0 and N0/e counts per minute at t = 5 minutes. The time (in minutes) at which the activity reduces to half its value is [2010]
The binding energy per nucleon in deuteriumand helium nuclei are 1.1 MeV and 7.0 MeV,respectively. When two deuterium nuclei fuseto form a helium nucleus the energy released inthe fusion is :
The decay constant of a radio isotope is λ. If A1 and A2 are its activities at times t1 and t2 respectively, the number of nuclei which have decayed during the time (t1 – t2) :
The half life of a radioactive isotope 'X' is 50 years. It decays to another element 'Y' which isstable. The two elements 'X' and 'Y' were foundto be in the ratio of 1 : 15 in a sample of agiven rock. The age of the rock was estimatedto be [2011]
The power obtained in a reactor using U235 disintegration is 1000 kW. The mass decay of U235 per hour is [2011]
A radioactive nucleus of mass M emits a photonof frequency μ and the nucleus recoils. The recoilenergy will be [2011]
A nucleus  emits one α-particle and two β-particles. The resulting nucleus is [2011]
emits one α-particle and two β-particles. The resulting nucleus is [2011]
Fusion reaction takes place at high temperaturebecause [2011]
Two radioactive nuclei P and Q, in a given sample decay into a stable nucleolus R. At time t = 0, number of P species are 4 N0 and that of Q are N0. Half-life of P (for conversion to R) is 1 minute where as that of Q is 2 minutes. Initially there are no nuclei of R present in the sample. When number of nuclei of P and Q are equal, the number of nuclei of R present in the sample would be [2011M]
If the nuclear radius of 27Al is 3.6 Fermi, the approximate nuclear radius of 64Cu in Fermi is : [2012]
A mixture consists of two radioactive materials A1 and A2 with half lives of 20 s and 10 srespectively. Initially the mixture has 40 g of A1 and 160 g of A2. The amount of the two in themixture will become equal after : [2012]
The half life of a radioactive nucleus is 50 days. The time interval (t2 – t1) between the time t2 when 2/3 of its has decayed and the time t1 when 1/3 of it had decayed is : [2012]
A certain mass of Hydrogen is changed to Heliumby the process of fusion. The mass defect infusion reaction is 0.02866 a.m.u. The energyliberated per a.m.u. is(Given : 1 a.m.u = 931 MeV) [NEET 2013]
The half life of a radioactive isotope ‘X’ is20 years. It decays to another element ‘Y’ whichis stable. The two elements ‘X’ and ‘Y’ were foundto be in the ratio of 1 : 7 in a sample of a thegiven rock. The age of the rock is estimated tobe [NEET 2013]
α-particles, β-particles and γ-rays are all havingsame energy. Their penetrating power in a givenmedium in increasing order will be [NEET Kar. 2013]
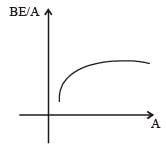
How does the binding energy per nucleon varywith the increase in the number of nucleons ? [NEET Kar. 2013]
|
98 videos|334 docs|102 tests
|


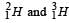 requires a and b amount of energies for their nucleons to be separated.
requires a and b amount of energies for their nucleons to be separated.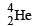 releases c amount of energy in its formation i.e., in assembling the nucleons as nucleus.
releases c amount of energy in its formation i.e., in assembling the nucleons as nucleus.
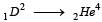
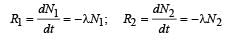
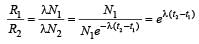
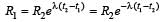
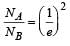
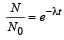
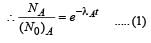
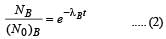
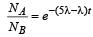
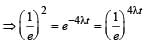
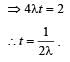
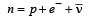
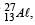 let nuclear radius be R1
let nuclear radius be R1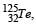 nuclear radius be R2
nuclear radius be R2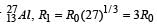
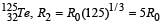
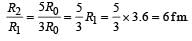
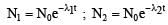
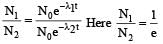
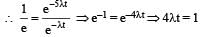
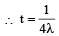
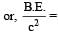 ZMp + (A–Z) Mn–M(A,Z)
ZMp + (A–Z) Mn–M(A,Z)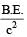
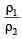
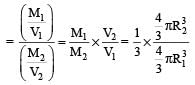
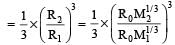
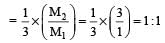
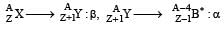
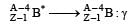
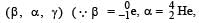 mass number and charge number of a nucleus remains unchanged during γ decay)
mass number and charge number of a nucleus remains unchanged during γ decay)
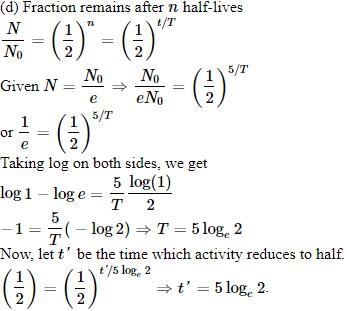
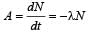
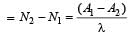
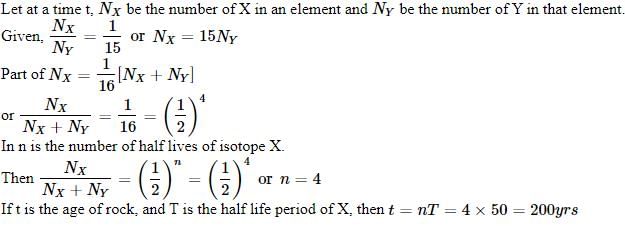
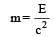
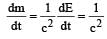 (Power in watt)
(Power in watt)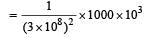
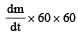
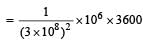 = 4 × 10–8 kg
= 4 × 10–8 kg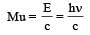
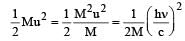
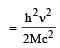

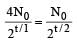
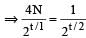
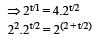
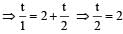
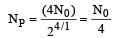
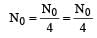
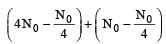
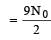
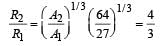
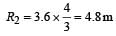
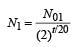
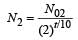
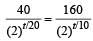
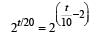
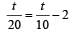
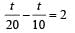
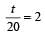
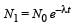
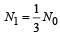
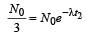
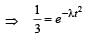 ...(i)
...(i)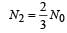
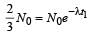
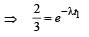 ...(ii)
...(ii)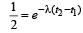
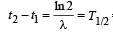 = 50 days
= 50 days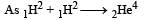
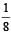
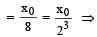 t = 3T = 3 × 20 = 60
t = 3T = 3 × 20 = 60