Test: MCQs (One or More Correct Option): Waves | JEE Advanced - ENGAA MCQ
25 Questions MCQ Test - Test: MCQs (One or More Correct Option): Waves | JEE Advanced
A wave equation which gives the displacement along the y-direction is given by y = 10–4 sin (60t + 2x) where x and y are in metres and t is time in seconds. This represents a wave
A transver se wave is described by the equation 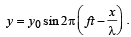 The maximum particle velocity is equal to four times the wave velocity if
The maximum particle velocity is equal to four times the wave velocity if
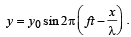 The maximum particle velocity is equal to four times the wave velocity if
The maximum particle velocity is equal to four times the wave velocity if An air column in a pipe, which is closed at one end, will be in resonance with a vibrating tuning fork of frequency 264 Hz if the length of the column in cm is :
A tube, closed at one end and containing air, produces, when excited, the fundamental note of frequency 512 Hz. If the tube is open at both ends the fundamental frequency that can be excited is (in Hz)
The displacement of particles in a string stretched in the x-direction is represented by y. Among the following expressions for y, those describing wave motion are :
An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.
The ratio of the length of P1 to that of P2 is
Velocity of sound in air is 320 m/s. A pipe closed at one end has a length of 1 m. Neglecting end corrections, the air column in the pipe can resonate for sound of frequency :
A wave is represented by the equation

where x is in meters and t is in seconds. The expression represents :
Two identical straight wires are stretched so as to produce 6 beats per second when vibrating simultaneously. On changing the tension slightly in one of them, the beat frequency remains unchanged. Denoting by T1 , T2 the higher and the lower initial tension in the strings, then it could be said that while making the above changes in tension,
The displacement y of a particle executing periodic motion is given by 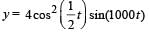
This expression may be considereed to be a result of the superposition of
A sound wave of frequency f travels horizontally to the right. It is reflected from a large vertical plane surface moving to left with a speed v. The speed of sound in medium is C
A string of length 0.4 m and mass 10–2 kg is tightly clamped at its ends. The tension in the string is 1.6 N. Identical wave pulses are produced at one end at equal intervals of time, Δt. The minimum value of Δt which allows constructive interference between successive pulses is
The (x, y) co-ordinates of the corners of a square plate are (0, 0), (L, 0), (L, L) and (0, L). The edges of the plate are clamped and transverse standing waves are set up in it. If u(x, y) denotes the displacement of the plate at the point (x, y) at some instant of time, the possible expression(s) for u is (are) (a = positive constant)
A transverse sinusoidal wave of amplitude a, wavelength l and frequency f is travelling on a stretched string. The maximum speed of any point on the string is v/10, where v is the speed of propagation of the wave. If a = 10–3m and v = 10 m s–1, then λ and f are given by
y(x, t) = 0.8/[4x+5t)2+5] represents a moving pulse, where x and y are in meter and t in second. Then
In a wave motion y = a sin (kx - ωt), y can represent
Standing waves can be produced
As a wave propagates,
A student performed the experiment to measure the speed of sound in air using resonance air-column method. Two resonances in the air-column were obtained by lowering the water level. The resonance with the shorter air-column is the first resonance and that with the longer air-column is the second resonance. Then,
A person blows into open-end of a long pipe. As a result, a high pressure pulse of air travels down the pipe.
When this pulse reaches the other end of the pipe,
A horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation, y(x, t) = (0.01 m) sin [(62.8 m–1)x] cos[(628 s–1)t]. Assuming π = 3.14, the correct statement(s) is (are)
Two vehicles, each moving with speed u on the same horizontal straight road, are approaching each other. Wind blows along the road with velocity w. One of these vehicles blows a whistle of frequency f1. An observer in the other vehicle hears the frequency of the whistle to be f2. The speed of sound in still air is V. The correct statement(s) is (are)
A student is performing an experiment using a resonance column and a tuning fork of frequency 244 s–1. He is told that the air in the tube has been replaced by another gas (assume that the column remains filled with the gas). If the minimum height at which resonance occurs is (0.350 ± 0.005) m, the gas in the tube is
(Useful information: 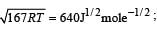
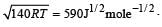 The molar masses M in grams are given in the options. Take the values of
The molar masses M in grams are given in the options. Take the values of 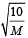 for eachgas as given there.)
for eachgas as given there.)
One end of a taut string of length 3 m along the x-axis is fixed at x = 0. The speed of the waves in the string is 100 ms–1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible waveform (s) of these stationary waves is(are)
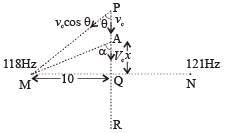
Two loudspeakers M and N are located 20 m apart and emit sound at frequencies 118 Hz and 121 Hz, respectively. A car is initially at a point P , 1800 m away from the midpoint Q of the line MN and moves towards Q constantly at 60 km/hr along the perpendicular bisector of MN. It crosses Q and eventually reaches a point R, 1800 m away from Q. Let v(t) represent the beat frequency measured by a person sitting in the car at time t. Let vP , vQ and vR be the beat frequencies measured at locations P, Q and R, respectively. The speed of sound in air is 330 ms–1. Which of the following statement(s) is(are) true regarding the sound heard by the person?



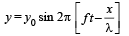
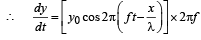
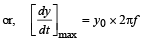
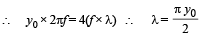


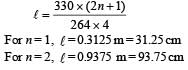
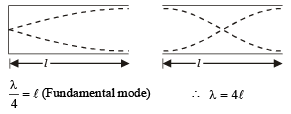

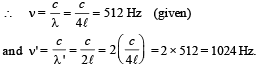

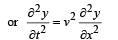 ....(i)
....(i)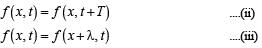
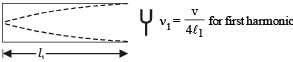

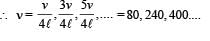
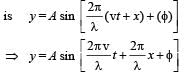
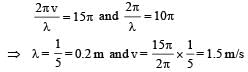
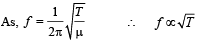

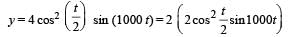
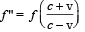
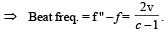
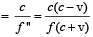
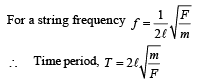
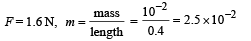
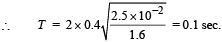
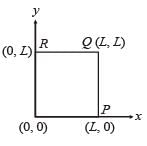
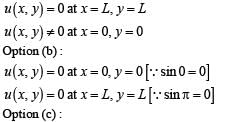
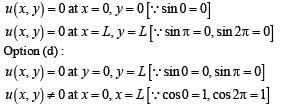
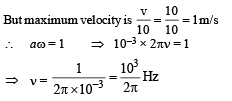
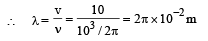
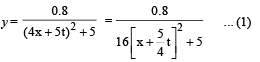
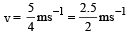
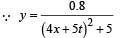
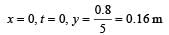
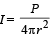
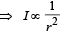



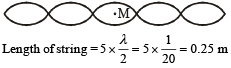
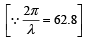
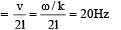


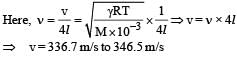
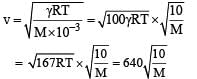
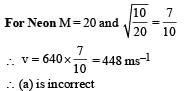
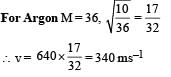
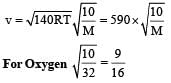
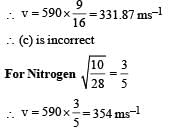
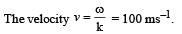
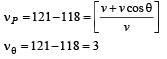
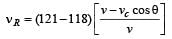
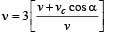
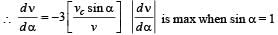
 … (ii)
… (ii)
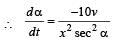 …(iii)
…(iii)