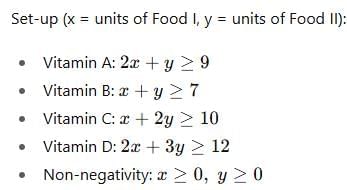Test: Inequalities- 3 - CA Foundation MCQ
10 Questions MCQ Test Quantitative Aptitude for CA Foundation - Test: Inequalities- 3
(i) An employer recruits experienced (x) and fresh workmen (y) for his firm under the condition that he cannot employ more than 9 people. x and y can be related by the inequality
On the average experienced person does 5 units of work while a fresh one 3 units of work daily but the employer has to maintain an output of at least 30 units of work per day. This situation can be expressed as
The rules and regulations demand that the employer should employ not more than 5 experienced hands to 1 fresh one and this fact can be expressed as
The union however forbids him to employ less than 2 experienced person to each fresh person. This situation can be expressed as
The graph to express the inequality y ≤ (½)x is indicated by
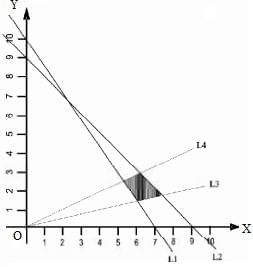
L1 : 5x + 3y = 30 L2 : x+y = 9 L3 : y = x/3 L4 : y = x/2 The common region (shaded part) shown in the diagram refers to
A dietitian wishes to mix together two kinds of food so that the vitamin content of the mixture is at least 9 units of vitamin A, 7 units of vitamin B, 10 units of vitamin C and 12 units of vitamin D. The vitamin content per Kg. of each food is shown below: A B C D Food I : 2 1 1 2 Food II: 1 1 2 3 Assuming x units of food I is to be mixed with y units of food II the situation can be expressed as
Graphs of the inequations are drawn below:
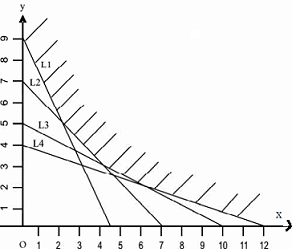
L1 : 2x +y = 9 L2 : x + y = 7 L3 : x+2y= 10 L4 : x + 3y = 12
The common region indicated on the diagram is expressed by the set of inequalities
|
101 videos|277 docs|89 tests
|