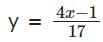Test: Inequalities- 1 - CAT MCQ
10 Questions MCQ Test Quantitative Aptitude (Quant) - Test: Inequalities- 1
Let a, b, c, d be four integers such that a + b + c + d = 4m + 1 where m is a positive integer. Given m, which one of the following is necessarily true?
If x > 5 and y < -1, then which of the following statements is true?
If a, b, c and d are four positive real numbers such that abcd = 1, what is the minimum value of (1 + a)(1 + b)(1 + c)(1+ d)?
If x, y and z are real numbers such that x + y + z = 5 and xy + yz + zx = 3, what is the largest value that x can have?
The number of integers n satisfying -n + 2 ≥ 0 and 2n ≥ 4 is
x, y and z are three positive integers such that x > y > z. Which of the following is closest to the product xyz?
Let le(a, b, c) mean “the least (minimum) of a, b, c” and ma(a, b, c) mean “the greatest (maximum) of a, b, c”.
For x = 15, y = 10, z = 9, find the value of:
le(x, min(y, x - z), le(9, 8, ma(x, y, z))).
The number of positive integer valued pairs (x, y), satisfying 4x – 17 y = 1 and x < 1000 is:
p, q and r are three non-negative integers such that p + q + r = 10. The maximum value of pq + qr + pr + pqr is
|
188 videos|177 docs|103 tests
|