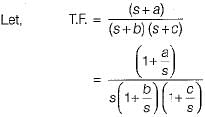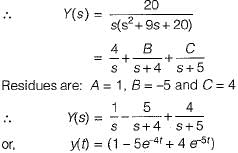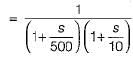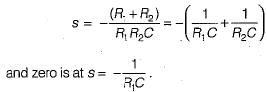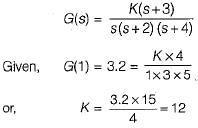Test: Transfer Function - 2 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: Transfer Function - 2
Non-minimum phase transfer function is defined as the transfer function
The type and order of the system described by the open loop transfer function 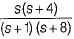 are respectively
are respectively
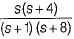 are respectively
are respectivelyAssertion (A): If the number of zeros are less than the number of poles (i.e. Z < P), we say that there are zeros at infinity and the order of such zeros is P-Z
Reason (R): The value of the transfer function becomes zero for s tends to zero.
Reason (R): The value of the transfer function becomes zero for s tends to zero.
The principle of homogeneity and superposition are applied to
The differential equation of a control system having input x(t) and output y(t) is given as
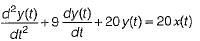
The output response of the system for unit step input is given by
The step response of a system is given by
c(t) = 1 + 0.25 e-50t - 1.25e-10t
The steady state gain of the transfer function in time constant form will be
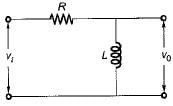
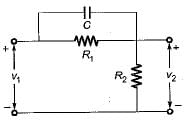
The poles and zeros of the transfer function 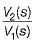 for the network shown below are located at
for the network shown below are located at
The pole-zero configuration of a transfer function is shown below:
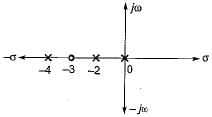
If the value of the transfer function at s = 1 is 3.2, the gain factor K is
|
25 docs|263 tests
|