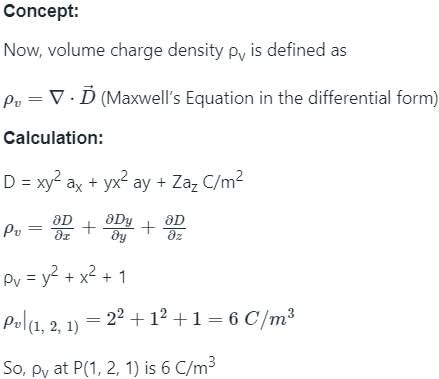Test: Electrostatics - Electrical Engineering (EE) MCQ
20 Questions MCQ Test GATE Electrical Engineering (EE) Mock Test Series 2026 - Test: Electrostatics
A spherical surface of radius of 3 mm is centered at P(4, 1, 5) in free space. If D = xux C/m2 the net electric flux leaving the spherical surface is
What is the volume charge density at point P(1, 2, 1) associated with electric flux field D = xy2ax + yx2ay + z az C/m2
If D = 2rur C/m2, the total electric flux leaving the surface of the cube, 0
< x , y, z < 0.4 is
E = 4ux -3 uy + 5uz in the neighborhood of point P(6, 2, -3). The incremental work done in moving 5 C charge a distance of 2 m in the direction ux + uy + uz is
If E = 100up V /m , the incremental amount of work done in moving a 60 μC charge a distance of 2 mm from P(1, 2, 3) toward Q(2, 1, 4) is
A 10 C charge is moved from the origin to P(3, 1, -1) in the field E = 2xux - 3y2 uy + 4uz V/m along the straight line path x = -3y, y = x + 2z. The amount of energy required is
A uniform surface charge density of 30 nC /m2 is present on the spherical surface r = 6 mm in free space. The VAB between A (r = 2 cm, θ = 350 , Ø = 550 ) and B (r = 3 cm, θ = 400 , Ø = 900 )
A point charge is located at the origin in free space. The work done in carrying a charge 10 C from point A (r = 4 cm, θ = π/6 , Ø = π/4) to B (r = 4 cm, θ = π/3 , Ø = π/6) is
Let a uniform surface charge density of 5 nC/m2 be present at the z = 0 plane, a uniform line charge density of 8 nC/m be located at x = 0, z = 4 and a point charge of 2 μC be present at P(2, 0, 0). If V = 0 at A(0, 0, 5), the V at B(1, 2, 3) is
A non uniform linear charge density, ρL = 6/ (z2 + 1) nC/m lies along the z axis. The potential at P(ρ = 1, 0, 0) in free space is (V∞ = 0 )
The annular surface, 1 cm < ρ < 3 cm carries the nonuniform surface charge density ρs = 5ρ nC/m2. The V at P(0, 0, 2 cm) is
If V = 2xy2z3 + 3ln(x2 + 2y2 + 3z2 ) in free space the magnitude of electric field E at P (3, 2, -1) is
It is known that the potential is given by V = 70 r0.6 V. The volume charge density at r = 0.6 m is
The potential field V = 80r2 cosθ V. The volume charge density at point P(2.5, θ = 300 , Ø = 600 ) in free space is
Within the cylinder ρ = 2, 0 < z <1 the potential is given by V = 100 + 50ρ +150ρ sinØ V. The charge lies within the cylinder is
A dipole having
is located at the origin in free space and aligned so that its moment is in the uz direction. The E at point (r = 1, 450 ,Ø = 0) is
A dipole located at the origin in free space has a moment p = 2 x 10-9 uz c.m. The points at which |E|θ = 1 mV m on line y = z , x = 0 are
A dipole having a moment p = 3ux - 5uy + 10uz nC.m is located at P(1, 2,-4) in free space. The V at Q (2, 3, 4) is
A potential field in free space is expressed as V =40/xyz . The total energy stored within the cube 1 < x, y, z < 2 is
Four 1.2 nC point charge are located in free space at the corners of a square 4 cm on a side. The total potential energy stored is
|
26 docs|257 tests
|
|
26 docs|257 tests
|