Test: Context Free Language- 1 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2026 Mock Test Series - Test: Context Free Language- 1
Which of the following languages is generated by the given grammar?
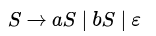
Consider the following languages:
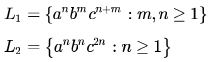
Which one of the following is TRUE?
02. Choose the correct alternatives (more than one may be correct) and write the corresponding letters only: (xix) Context-free languages are
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only:
If G is a context free grammar and is a string of lengthl in L(G), how long is a derivation of ω in G, if G is in Chomsky normal form?
Which of the following definitions below generate the same language as L , where
If L1 and L2 are context free languages and a regular set, one of the languages below is not necessarily a context free language. Which one?
Define a context free languages for some υ in
( in other words, (L) is the set of prefixes of L).
Let is nonempty snd has an equal number of 0's and 1's}
Then is
|
57 docs|215 tests
|
|
57 docs|215 tests
|



















