Test: Propositional & First Order Logic- 1 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: Propositional & First Order Logic- 1
What is the logical translation of the following statement?
"None of my friends are perfect."
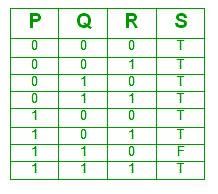
Let # be a binary operator defined as X # Y = X′ + Y′ where X and Y are Boolean variables. Consider the following two statements.
S1: (P # Q) # R = P # (Q # R)
S2: Q # R = R # Q
Which of the following is/are true for the Boolean variables P, Q and R?
What is the correct translation of the following statement into mathematical logic?
“Some real numbers are rational”
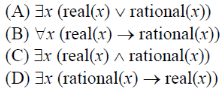
Which one of the following options is CORRECT given three positive integers x, y and z, and a predicate?
P(x) = ¬(x=1)∧∀y(∃z(x=y*z)⇒(y=x)∨(y=1))
Suppose the predicate F(x, y, t) is used to represent the statement that person x can fool person y at time t. which one of the statements below expresses best the meaning of the formula ∀x∃y∃t(¬F(x, y, t))?
Which one of the following is the most appropriate logical formula to represent the statement? "Gold and silver ornaments are precious". The following notations are used: G(x): x is a gold ornament S(x): x is a silver ornament P(x): x is precious
In propositional logic P ↔ Q is equivalent to (Where ~ denotes NOT):
Q. Which of the above two are equivalent?
Let fsa and pda be two predicates such that fsa(x) means x is a finite state automaton, and pda(y) means that y is a pushdown automaton. Let equivalent be another predicate such that equivalent (a, b) means a and b are equivalent. Which of the following first order logic statements represents the following: Each finite state automaton has an equivalent pushdown automaton.
P and Q are two propositions. Which of the following logical expressions are equivalent?
Let Graph(x) be a predicate which denotes that x is a graph. Let Connected(x) be a predicate which denotes that x is connected. Which of the following first order logic sentences DOES NOT represent the statement: “Not every graph is connected”?
Which of the following is TRUE about formulae in Conjunctive Normal Form?
The following propositional statement is (P → (Q v R)) → ((P ^ Q) → R)
Which one of the following Boolean expressions is NOT a tautology?
The CORRECT formula for the sentence, “not all rainy days are cold” is
Which one of the first order predicate calculus statements given below correctly express the following English statement?
Tigers and lions attack if they are hungry or threatened.
Consider the following propositional statements:
P1 : ((A ∧ B) → C)) ≡ ((A → C) ∧ (B → C))
P2 : ((A ∨ B) → C)) ≡ ((A → C) ∨ (B → C))
which one of the following is true?
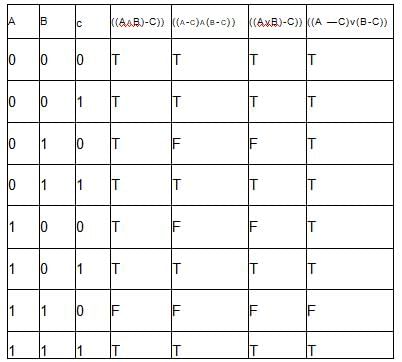
A logical binary relation □ ,is defined as follows
Q. Let ~ be the unary negation (NOT) operator, with higher precedence than □. Which one of the following is equivalent to A∧B ?
Let P, Q and R be three atomic prepositional assertions. Let X denote (P v Q) → R and Y denote (P → R) v (Q → R). Which one of the following is a tautology?
What is the first order predicate calculus statement equivalent to the following?
Every teacher is liked by some student