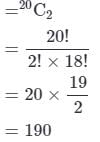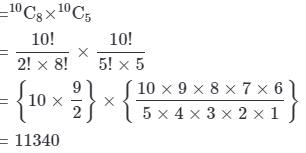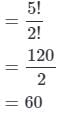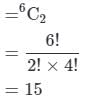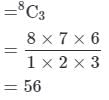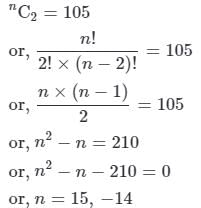MCQ: Permutations and Combinations - 2 - SSC CGL MCQ
15 Questions MCQ Test SSC CGL Tier 2 - Study Material, Online Tests, Previous Year - MCQ: Permutations and Combinations - 2
How many different words can be formed using all the letters of the word ALLAHABAD?
(a) When vowels occupy the even positions.
(b) Both L do not occur together.
(a) When vowels occupy the even positions.
(b) Both L do not occur together.
In how many ways 4 boys and 3 girls can be seated in a row so that they are alternate.
In how many ways 2 students can be chosen from the class of 20 students?
A question paper has two parts, A and B, each containing 10 questions. If a student has to choose 8 from part A and 5 from part B, in how many ways can he choose the questions?
How many Permutations of the letters of the word APPLE are there?
In how many ways can 10 examination papers be arranged so that the best and the worst papers never come together?
A two member committee comprising of one male and one female member is to be constitute out of five males and three females. Amongst the females. Ms. A refuses to be a member of the committee in which Mr. B is taken as the member. In how many different ways can the committee be constituted ?
Three gentlemen and three ladies are candidates for two vacancies. A voter has to vote for two candidates. In how many ways can one cast his vote?
Find the number of triangles which can be formed by joining the angular points of a polygon of 8 sides as vertices.
There are 10 points in a plane out of which 4 are collinear. Find the number of triangles formed by the points as vertices.
The number of positive integers which can be formed by using any number of digits from 0, 1, 2, 3, 4, 5 without repetition.
A letter lock consists of 4 rings, each ring contains 9 non-zero digits. This lock can be opened by setting four digit code with the proper combination of each of the 4 rings. Maximum how many codes can be formed to open the lock ?
How many ways can 4 prizes be given away to 3 boys, if each boy is eligible for all the prizes?
In a party every person shakes hands with every other person. If there are 105 hands shakes, find the number of person in the party.
In the next World cup of cricket there will be 12 teams, divided equally in two groups. Teams of each group will play a match against each other. From each group 3 top teams will qualify for the next round. In this round each team will play against each others once. Four top teams of this round will qualify for the semifinal round, where they play the best of three matches. The Minimum number of matches in the next World cup will be:
|
1366 videos|1313 docs|1016 tests
|
|
1366 videos|1313 docs|1016 tests
|


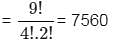
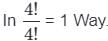
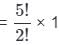 = 60 ways.
= 60 ways.