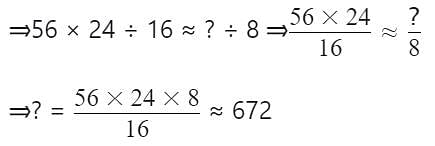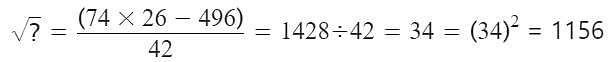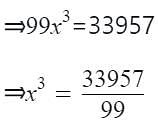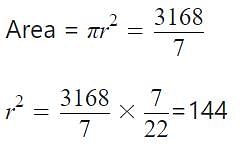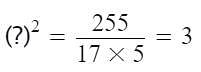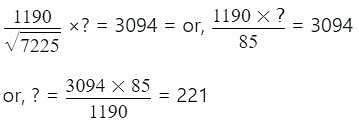SSC CGL Exam > SSC CGL Tests > SSC CGL Tier 2 - Study Material, Online Tests, Previous Year > MCQ: Square Roots and Cube Roots - 2 - SSC CGL MCQ
MCQ: Square Roots and Cube Roots - 2 - SSC CGL MCQ
Test Description
15 Questions MCQ Test SSC CGL Tier 2 - Study Material, Online Tests, Previous Year - MCQ: Square Roots and Cube Roots - 2
MCQ: Square Roots and Cube Roots - 2 for SSC CGL 2025 is part of SSC CGL Tier 2 - Study Material, Online Tests, Previous Year preparation. The MCQ: Square Roots and Cube Roots - 2 questions and answers have been
prepared according to the SSC CGL exam syllabus.The MCQ: Square Roots and Cube Roots - 2 MCQs are made for SSC CGL 2025 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for MCQ: Square Roots and Cube Roots - 2 below.
Solutions of MCQ: Square Roots and Cube Roots - 2 questions in English are available as part of our SSC CGL Tier 2 - Study Material, Online Tests, Previous Year for SSC CGL & MCQ: Square Roots and Cube Roots - 2 solutions in
Hindi for SSC CGL Tier 2 - Study Material, Online Tests, Previous Year course. Download more important topics, notes, lectures and mock
test series for SSC CGL Exam by signing up for free. Attempt MCQ: Square Roots and Cube Roots - 2 | 15 questions in 15 minutes | Mock test for SSC CGL preparation | Free important questions MCQ to study SSC CGL Tier 2 - Study Material, Online Tests, Previous Year for SSC CGL Exam | Download free PDF with solutions
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 1
MCQ: Square Roots and Cube Roots - 2 - Question 2
Which of the following numbers are divisible by 3 but not by 9?
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 2
MCQ: Square Roots and Cube Roots - 2 - Question 3
The least number to be subtracted from 24136 to make it a perfect square
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 3
MCQ: Square Roots and Cube Roots - 2 - Question 4
The difference of the squares of two consecutive even integers is divisible by which of the following integers?
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 4
MCQ: Square Roots and Cube Roots - 2 - Question 5
What is the least number to be added to 2000 to make it a perfect square?
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 5
MCQ: Square Roots and Cube Roots - 2 - Question 6
If the number 517 * 324 is completely divisible by 3, then the smallest whole number in place of * will be?
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 6
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 7
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 8
MCQ: Square Roots and Cube Roots - 2 - Question 9
The three numbers are in the ratio 2 : 3 : 4. The sum of their cubes is 33957. The numbers are,
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 9
MCQ: Square Roots and Cube Roots - 2 - Question 10
The area of a circular play ground is 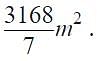 The diameter of the ground is
The diameter of the ground is
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 10
MCQ: Square Roots and Cube Roots - 2 - Question 11
The square of a natural number when subtracted from its cube results in 48. The number is
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 11
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 12
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 13
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 14
Detailed Solution for MCQ: Square Roots and Cube Roots - 2 - Question 15
|
1366 videos|1313 docs|1016 tests
|
Information about MCQ: Square Roots and Cube Roots - 2 Page
In this test you can find the Exam questions for MCQ: Square Roots and Cube Roots - 2 solved & explained in the simplest way possible.
Besides giving Questions and answers for MCQ: Square Roots and Cube Roots - 2, EduRev gives you an ample number of Online tests for practice
|
1366 videos|1313 docs|1016 tests
|
Download as PDF