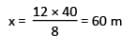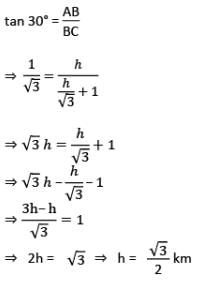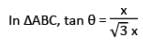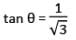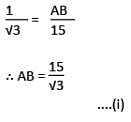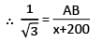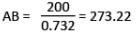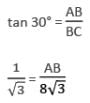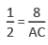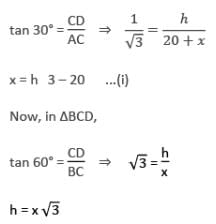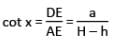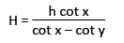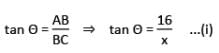MCQ Test: Height & Distance - 1 - SSC CGL MCQ
15 Questions MCQ Test SSC CGL Tier 2 - Study Material, Online Tests, Previous Year - MCQ Test: Height & Distance - 1
A vertical stick 12 cm long casts a shadow 8 cm long on the ground. At the same time, a tower casts a shadow 40 m long on the ground. The height of the tower is
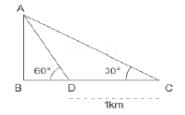
If the anlge of elevation of a balloon from two consecutive km stones along a road are 30 degree and 60 degree respectively, then the height of the balloon above the ground will be
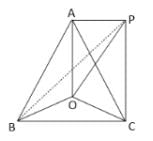
A pole stands vertically, inside a saclene triangular park ABC, if the angle of elevation of the top of the pole from each corner of the park is same, then in ΔABC, the foot of the pole is at the
Two poles of heights 6 m and 11 m stand vertically upright on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?
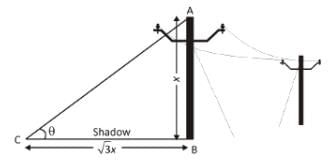
At an instant, the length of the shadow of a pole is square root of 3 times the height of the pole. Find the angle of elevation of the turn.
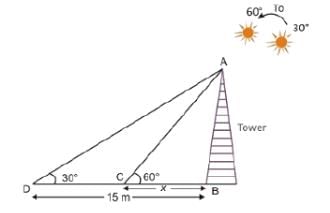
The shadow of a tower is 15 m when the sun’s elevation is 30°. What is the length of the shadow when the sun’s elevation is 60°?
A telegraph post gets broken at a point against a storm and its top touches the ground at a distance 20 m from the base of the post making an angle 30° with the ground. What is the height of the post?
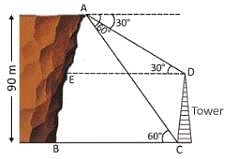
From the top of a cliff 90 m high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°, respectively. What is the height of the tower?
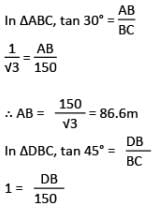
The angle of elevation of the top of an unfinished pillar at a point 150 m from its base is 30°. If the angle of elevation at the same point is to be 45°, then the pillar has to be raised to a height of how many metres?
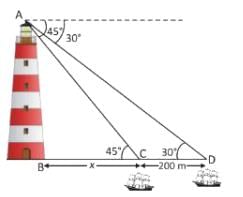
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 200 m apart, find the height of the light house.
A telegraph post is bent at a point above the ground due to storm. Its top just meets the ground at a distance of 8√3 meters from its foot and makes an angle of 30°, then the height of the post is :
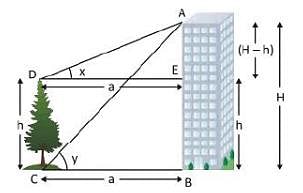
Two poles of equal height are standing opposite to each other on either side of a road which is 100 m wide. From a point between them on road, angle of elevation of their tops are 30° and 60°. The height of each pole (in metre) is
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 metres towards the foot of the tower to a point B, the angle of elevation increases to 60°. The height of the tower is
The angle of elevation of the top of a building from the top and bottom of a tree are x and y respectively. If the height of the tree is h metre, then (in metre) the height of the building is
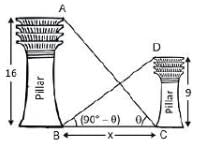
The distance between two pillars of length 16 metres and 9 metres is x metres. If two angles of elevation of their respective top from the bottom of the other are complementary to each other, then the value of x (in metres) is
|
1366 videos|1313 docs|1016 tests
|
|
1366 videos|1313 docs|1016 tests
|