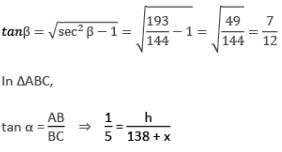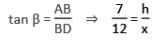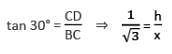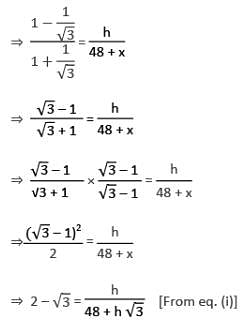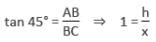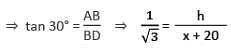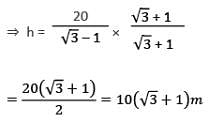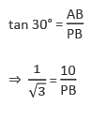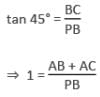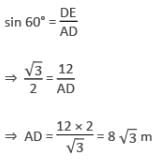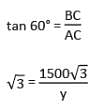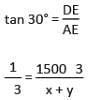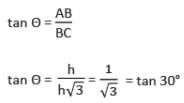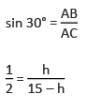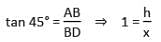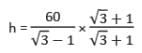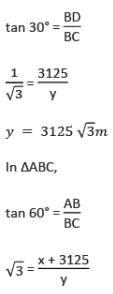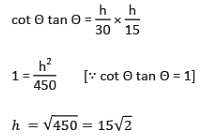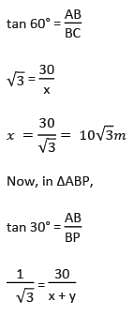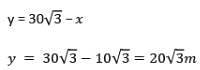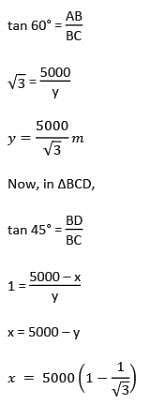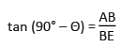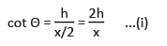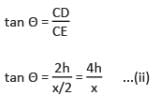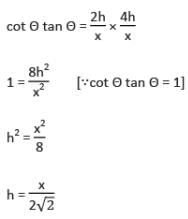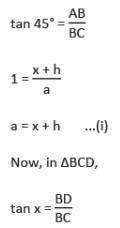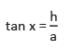MCQ Test: Heights and Distances - 2 - SSC CGL MCQ
15 Questions MCQ Test SSC CGL Tier 2 - Study Material, Online Tests, Previous Year - MCQ Test: Heights and Distances - 2
At a point on a horizontal line through the base of a monument, the angle of elevation of the top of the monument is found to be such that its tangent is 1/5. On walking 138 metres towards the monument the secant of the angle of elevation is found to be √(193) / 12. The height of the monument (in meter) is
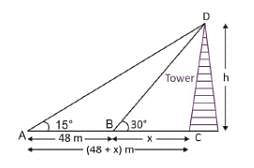
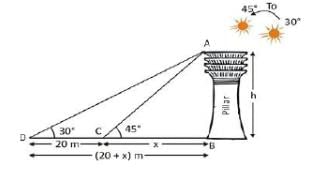
The angle of elevation of the top of a tower from two points A and B lying on the horizontal through the foot of the tower are respectively 15° and 30°. If A and B are on the same side of the tower and AB = 48 metre, then the height of the tower is :
If the angle of elevation of the sun changes from 30° to 45°, the length of the shadow of a pillar decreases by 20 metres. The height of the pillar is
From a point P on the ground the angles of elevation of the top of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from P is 45° Find the length of the flagstaff. (Take √3 = 1.732)
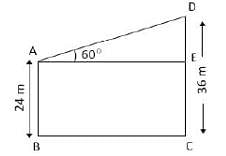
The top of two poles of height 24 m and 36 m are connected by a wire. If the wire makes an angle of 60° with the horizontal, then the length of the wire is
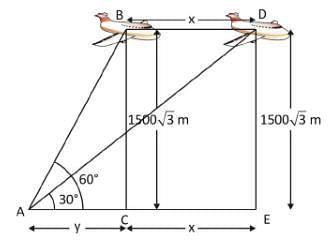
The angle of elevation of an aeroplane from a point on the ground is 60°. After 15 seconds flight, the elevation changes to 30°. If the aeroplane is flying at a height of 1500√3 m, find the speed of the plane.
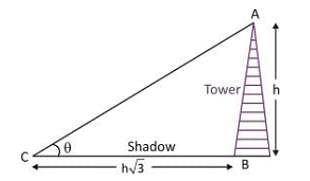
The shadow of a tower is √3 times its height. Then the angle of elevation of the top of the tower is
A vertical post 15 ft high is broken at a certain height and its upper part, not completely separated, meets the ground at an angle of 30°. Find the height at which the post is broken.
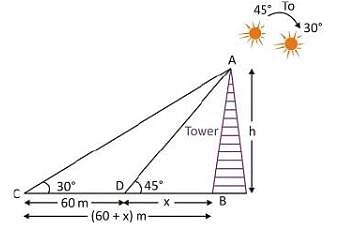
The shadow of the tower becomes 60 metres longer when the altitude of the sun changes from 45° to 30°. Then the height of the tower is
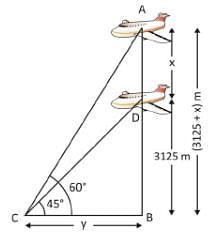
An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angle of elevation of the two planes from the same point on the ground are 30° and 60° respectively. The distance between the two planes at that instant is
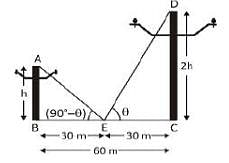
The distance between two vertical poles is 60 m. The height of one of the poles is double the height of the other. The angle of elevation of the top of the poles from the middle point of the line segment joining their feet are complementary to each other. The height of the poles are:
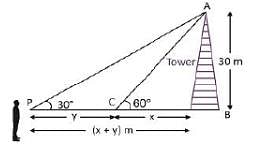
A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30°. The man walks some distance towards the tower and then his angle of elevation of the top of the tower is 60°. If the height of the tower is 30 m, then the distance he moves is
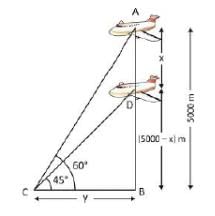
An aeroplane when flying at a height of 5000 m from the ground passes vertically above another aeroplane at an instant, when the angles of elevation of the two aeroplanes from the same point on the ground are 60° and 45° respectively. The vertical distance between the aeroplanes at that instant is
Two posts are x metres apart and the height of one is double that of the other. If from the mid-point of the line joining their feet, an observer finds the angular elevations of their tops to be complementary, then the height (in metres) of the shorter post is
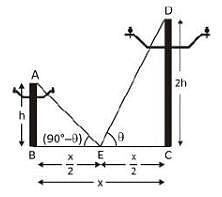
The angle of elevation of the top of a building and the top of the chimney on the roof of the building from a point on the ground are x° and 45° respectively. The height of building is h metre. Then the height of the chimney (in metre) is :
|
1366 videos|1313 docs|1016 tests
|
|
1366 videos|1313 docs|1016 tests
|