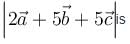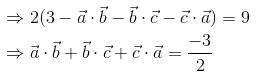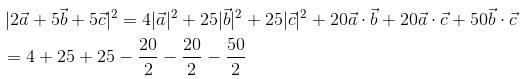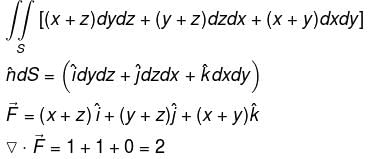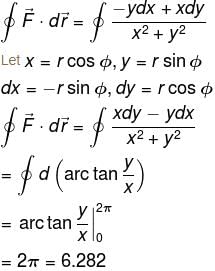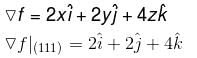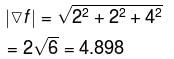Physics Exam > Physics Tests > Topic wise Tests for IIT JAM Physics > Vector Calculus NAT Level - 1 - Physics MCQ
Vector Calculus NAT Level - 1 - Physics MCQ
Test Description
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Vector Calculus NAT Level - 1
Vector Calculus NAT Level - 1 for Physics 2025 is part of Topic wise Tests for IIT JAM Physics preparation. The Vector Calculus NAT Level - 1 questions and answers have been
prepared according to the Physics exam syllabus.The Vector Calculus NAT Level - 1 MCQs are made for Physics 2025 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Vector Calculus NAT Level - 1 below.
Solutions of Vector Calculus NAT Level - 1 questions in English are available as part of our Topic wise Tests for IIT JAM Physics for Physics & Vector Calculus NAT Level - 1 solutions in
Hindi for Topic wise Tests for IIT JAM Physics course. Download more important topics, notes, lectures and mock
test series for Physics Exam by signing up for free. Attempt Vector Calculus NAT Level - 1 | 10 questions in 30 minutes | Mock test for Physics preparation | Free important questions MCQ to study Topic wise Tests for IIT JAM Physics for Physics Exam | Download free PDF with solutions
*Answer can only contain numeric values
Vector Calculus NAT Level - 1 - Question 1
 Evaluate the line integral
Evaluate the line integral  from (0, 0, 0) to (1, 1, 1) along the curve x = t, y = t2, z = t3
from (0, 0, 0) to (1, 1, 1) along the curve x = t, y = t2, z = t3
 Evaluate the line integral
Evaluate the line integral  from (0, 0, 0) to (1, 1, 1) along the curve x = t, y = t2, z = t3
from (0, 0, 0) to (1, 1, 1) along the curve x = t, y = t2, z = t3
Detailed Solution for Vector Calculus NAT Level - 1 - Question 1
*Answer can only contain numeric values
Vector Calculus NAT Level - 1 - Question 2
Compute the flux of 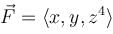 across the cone
across the cone 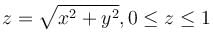 (upto three decimal places)
(upto three decimal places)
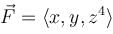 across the cone
across the cone 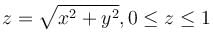 (upto three decimal places)
(upto three decimal places)
Detailed Solution for Vector Calculus NAT Level - 1 - Question 2
*Answer can only contain numeric values
Detailed Solution for Vector Calculus NAT Level - 1 - Question 3
*Answer can only contain numeric values
Vector Calculus NAT Level - 1 - Question 4
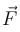 is a conservative field and potential
is a conservative field and potential  any curve C in the path from (0, 0, 1) to
any curve C in the path from (0, 0, 1) to 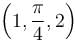 evaluate
evaluate 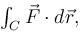 upto three decimal places.
upto three decimal places.
Detailed Solution for Vector Calculus NAT Level - 1 - Question 4
*Answer can only contain numeric values
Vector Calculus NAT Level - 1 - Question 5
If V = x2y2z2 the Laplacian of the field V at point 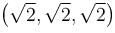 is :
is :
Detailed Solution for Vector Calculus NAT Level - 1 - Question 5
*Answer can only contain numeric values
Detailed Solution for Vector Calculus NAT Level - 1 - Question 6
*Answer can only contain numeric values
Detailed Solution for Vector Calculus NAT Level - 1 - Question 7
*Answer can only contain numeric values
Vector Calculus NAT Level - 1 - Question 8
S is the surface of sphere x2 + y2 + z2 = 9, the integral 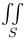 [(x + z) dydz + (y + z)dzdx + (x + y)dxdy] is equal to, (upto three decimal places)
[(x + z) dydz + (y + z)dzdx + (x + y)dxdy] is equal to, (upto three decimal places)
Detailed Solution for Vector Calculus NAT Level - 1 - Question 8
*Answer can only contain numeric values
Vector Calculus NAT Level - 1 - Question 9
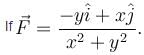 Evaluate
Evaluate 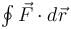 around any closed path C. (Ans. upto three decimal places)
around any closed path C. (Ans. upto three decimal places)
Detailed Solution for Vector Calculus NAT Level - 1 - Question 9
*Answer can only contain numeric values
Vector Calculus NAT Level - 1 - Question 10
If T(x, y, z) = x2 + y2 + 2z2 defines the temperature at any location (x, y, z) then the magnitude of the temperature gradient point P(1, 1, 1), (upto three decimal places)
Detailed Solution for Vector Calculus NAT Level - 1 - Question 10
Information about Vector Calculus NAT Level - 1 Page
In this test you can find the Exam questions for Vector Calculus NAT Level - 1 solved & explained in the simplest way possible.
Besides giving Questions and answers for Vector Calculus NAT Level - 1, EduRev gives you an ample number of Online tests for practice


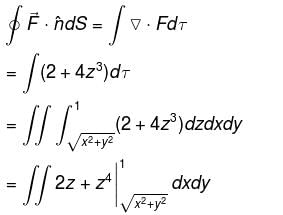
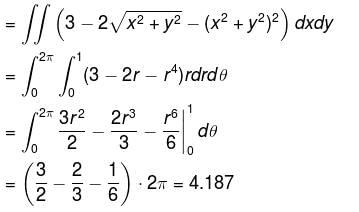

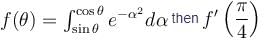
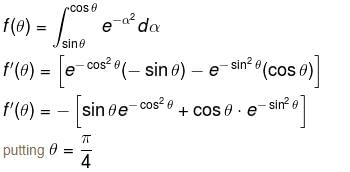
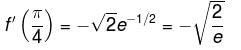
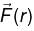

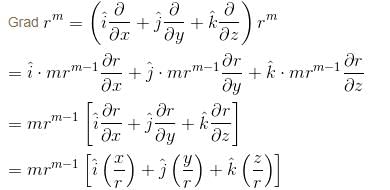
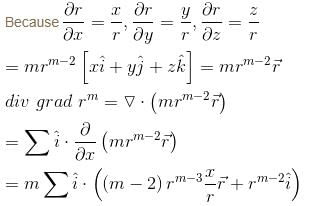
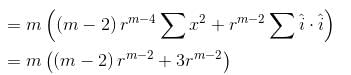
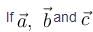 are unit vectors satisfying
are unit vectors satisfying  then
then