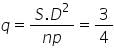Test: Binomial Distribution - JEE MCQ
10 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Binomial Distribution
A die is tossed twice. Getting a number greater than 4 is considered a success. Then the variance of the probability distribution of the number of successes is:
A man make attempts to hit the target. The probability of hitting the target is 3/5 . Then the probability that A hit the target exactly 2 times in 5 attempts is:
Trials of a random experiment are called Bernoulli trials, if they satisfy the condition/s:
In binomial probability distribution, mean is 3 and standard deviation is 3/2 . Then the probability distribution is:
A random variable is a real valued function whose domain is the.
In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is
The mean and variance of a binomial distribution are 4 and 3 respectively, then the probability of getting exactly six successes in this distribution is:
In a box of 10 electric bulbs, two are defective. Two bulbs are selected at random one after the other from the box. The first bulb is put back in the box before making the second selection. The probability that both the bulbs are not defective is:
Ten eggs are drawn successively with replacement from a lot containing 10% defective eggs. The probability that there is at least one defective egg is:
|
204 videos|290 docs|139 tests
|