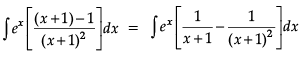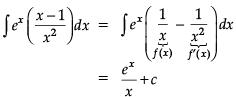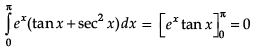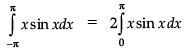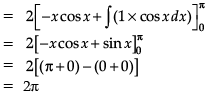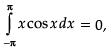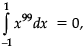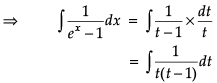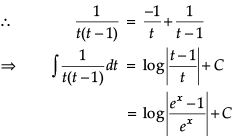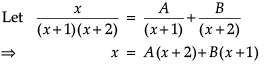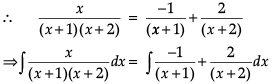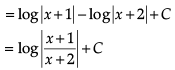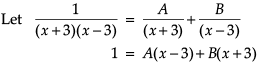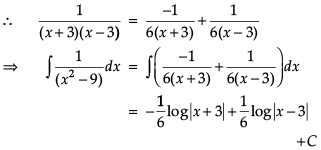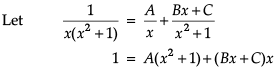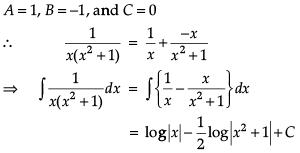Test: Integrals- Case Based Type Questions - Commerce MCQ
15 Questions MCQ Test - Test: Integrals- Case Based Type Questions
Read the following text and answer the following questions on the basis of the same:
∫ ex[f(x) +f′(x)]dx = ∫ exf(x)dx + ∫ex f′(x)dx
= f(x)ex – ∫ f ′(x)ex dx + ∫ f ′(x)ex dx
= ex f(x) + c
Q. ∫ ex (sinx + cos x)dx = _______.
Read the following text and answer the following questions on the basis of the same:
∫ ex[f(x) +f′(x)]dx = ∫ exf(x)dx + ∫ex f′(x)dx
= f(x)ex – ∫ f ′(x)ex dx + ∫ f ′(x)ex dx
= ex f(x) + c
Q. ∫ ex (x + 1) dx = _______.
Read the following text and answer the following questions on the basis of the same:
∫ ex[f(x) +f′(x)]dx = ∫ exf(x)dx + ∫ex f′(x)dx
= f(x)ex – ∫ f ′(x)ex dx + ∫ f ′(x)ex dx
= ex f(x) + c
Q. 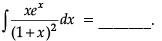
Read the following text and answer the following questions on the basis of the same:
∫ ex[f(x) +f′(x)]dx = ∫ exf(x)dx + ∫ex f′(x)dx
= f(x)ex – ∫ f ′(x)ex dx + ∫ f ′(x)ex dx
= ex f(x) + c
Q. ![]()
Read the following text and answer the following questions on the basis of the same:
∫ ex[f(x) +f′(x)]dx = ∫ exf(x)dx + ∫ex f′(x)dx
= f(x)ex – ∫ f ′(x)ex dx + ∫ f ′(x)ex dx
= ex f(x) + c
Q. ![]()
Read the following text and answer the following questions on the basis of the same:
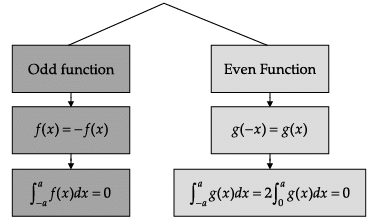
Q. ![]()
Read the following text and answer the following questions on the basis of the same:
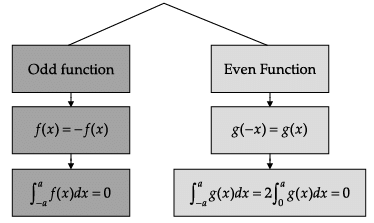
Q. ![]()
Read the following text and answer the following questions on the basis of the same:

Q. 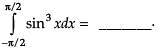
Read the following text and answer the following questions on the basis of the same:
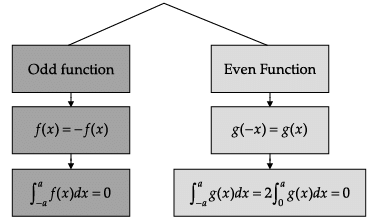
Q. ![]()
Read the following text and answer the following questions on the basis of the same:
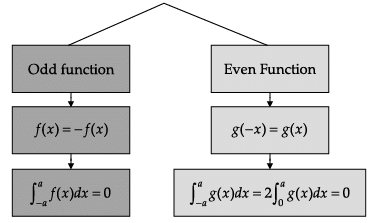
Q. 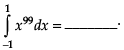
Read the following text and answer the following questions on the basis of the same:
Let’s say that we want to evaluate ∫[P(x)/Q(x)] dx, where P(x)/Q(x) is a proper rational fraction. In such cases, it is possible to write the integrand as a sum of simpler rational functions by using partial fraction decomposition. Post this, integration can be carried out easily. The following image indicates some simple partial fractions which can be associated with various rational functions:
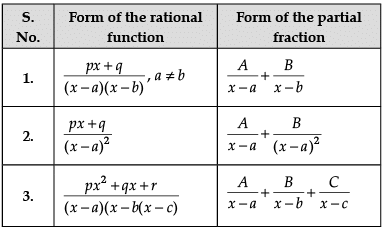
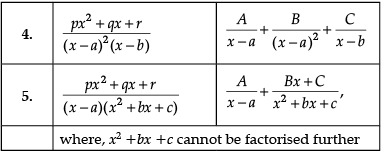
In the above table, A, B and C are real numbers to be determined suitably.
Q. ![]()
Read the following text and answer the following questions on the basis of the same:
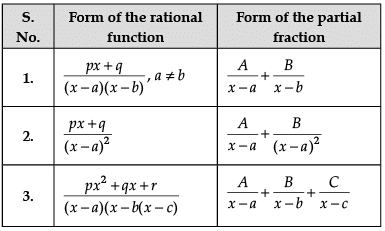
Let’s say that we want to evaluate ∫[P(x)/Q(x)] dx, where P(x)/Q(x) is a proper rational fraction. In such cases, it is possible to write the integrand as a sum of simpler rational functions by using partial fraction decomposition. Post this, integration can be carried out easily. The following image indicates some simple partial fractions which can be associated with various rational functions:
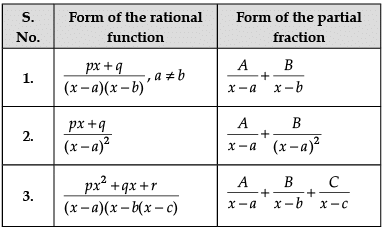
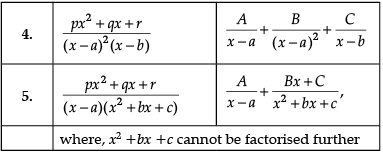
In the above table, A, B and C are real numbers to be determined suitably.
Q. Integration of ![]()
Read the following text and answer the following questions on the basis of the same:
Let’s say that we want to evaluate ∫[P(x)/Q(x)] dx, where P(x)/Q(x) is a proper rational fraction. In such cases, it is possible to write the integrand as a sum of simpler rational functions by using partial fraction decomposition. Post this, integration can be carried out easily. The following image indicates some simple partial fractions which can be associated with various rational functions:
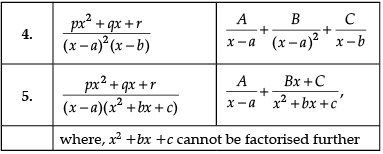
In the above table, A, B and C are real numbers to be determined suitably.
Q. ![]()
Read the following text and answer the following questions on the basis of the same:
Let’s say that we want to evaluate ∫[P(x)/Q(x)] dx, where P(x)/Q(x) is a proper rational fraction. In such cases, it is possible to write the integrand as a sum of simpler rational functions by using partial fraction decomposition. Post this, integration can be carried out easily. The following image indicates some simple partial fractions which can be associated with various rational functions:
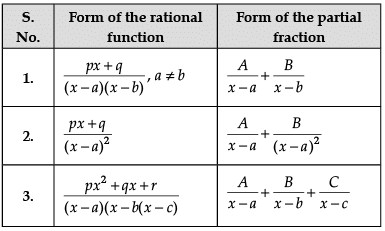
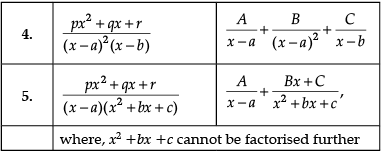
In the above table, A, B and C are real numbers to be determined suitably.
Q. ![]()
Read the following text and answer the following questions on the basis of the same:
Let’s say that we want to evaluate ∫[P(x)/Q(x)] dx, where P(x)/Q(x) is a proper rational fraction. In such cases, it is possible to write the integrand as a sum of simpler rational functions by using partial fraction decomposition. Post this, integration can be carried out easily. The following image indicates some simple partial fractions which can be associated with various rational functions:
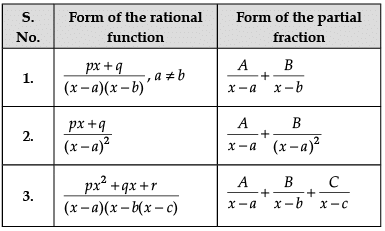
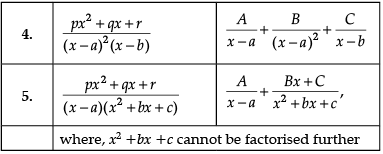
In the above table, A, B and C are real numbers to be determined suitably.
Q. ![]()