Courses

Test: Introduction To Conditional Probability


10 Questions MCQ Test Mathematics (Maths) Class 12 | Test: Introduction To Conditional Probability


Description
This mock test of Test: Introduction To Conditional Probability for JEE helps you for every JEE entrance exam. This contains 10 Multiple Choice Questions for JEE Test: Introduction To Conditional Probability (mcq) to study with solutions a complete question bank. The solved questions answers in this Test: Introduction To Conditional Probability quiz give you a good mix of easy questions and tough questions. JEE students definitely take this Test: Introduction To Conditional Probability exercise for a better result in the exam. You can find other Test: Introduction To Conditional Probability extra questions, long questions & short questions for JEE on EduRev as well by searching above.
QUESTION: 1

If A and B are two events of sample space S, then​

Solution: The probability of occurrence of event A under the condition that event B has already occurred& P(B)≠0 is called Conditional probability i.e; P(A|B)=P(A ∩ B)/P(B). Multiply with P(B) on both sides implies P(A ∩ B)=P(B).P(A|B). So option 'A' is correct.
QUESTION: 2

If E, F and G are events  with P(G) ≠≠ 0 then P ((E ∪ F)|G)  given by

Solution:
QUESTION: 3

If A, B and C are three events of sample space S, then​

Solution:
QUESTION: 4

If A and B are two events such that P(A) ≠ O and P(A) ≠ 1, then
Solution:

As we know that, P(A') = 1 - P(A)
P(A'⋂B') = P(AUB)' = 1 - P(AUB)
P(A'/B' ) = P(A'⋂B' ) / P(B') 
⇒ ( 1 - P(A U B )) / P(B')

QUESTION: 5

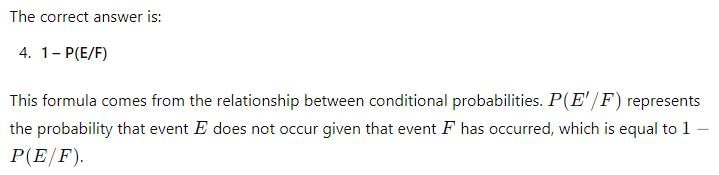
Let E and F be events of a sample space S of an experiment, then P(E’/F) = …​
Solution:
QUESTION: 6

A fair six-sided die is rolled twice. What is the probability of getting 2 on the first roll and not getting 4 on the second roll?
Solution:

The two events mentioned are independent. The first roll of the die is independent of the second roll. Therefore the probabilities can be directly multiplied.

P(getting first 2) = 1/6

P(no second 4) = 5/6

Therefore P(getting first 2 and no second 4) = 1/6* 5/6 = 5/36

QUESTION: 7

In a box containing 100 Ipods, 10 are defective. The probability that out of a sample of 5 Ipods, exactly 1 is defective is:
Solution:

r = 1, n = 5
p = 10/100  = 1/10,
q = 1 - p
q = 1 - 1/10   = 9/10
= nCr (p)r (q)(n - r)
Exactly one is defective = 5C1 (1/10)1 (9/10)(5 - 1)
= 5C1 (1/10) (9/10)4
= (1/2) (9/10)4

QUESTION: 8

Three coins are tossed. If at least two coins show head, the probability of getting one tail is:​
Solution:

Subset={HHH , HHT,HTH,HTT,THH,THT,TTH,TTT}
P(at least two head) = 4/8 = ½
Getting(one tail) = {HHT, HTH, THH} 
= 3/8
Therefore, P(one tail) = (⅜) / (½) 
= ¾

QUESTION: 9

If A and B are two events such that P(A) = 0.3 and P(B) = 0.9 and P(B|A) = 0.6,then P(A|B) = ……​
Solution:

P(B/A) = P(A∩B)/P(A)
​P(A∩B) = P(B/A))×P(A)
=0.6×0.3
=0.18
P(A∩B) = P(A/B))×P(B)
0.18 = P(A/B) * 0.9
 P(A/B) = 0.2

QUESTION: 10

A bag contains 25 tickets numbered from 1 to 25. Two tickets are drawn one after another without replacement. The probability that both tickets will show even numbers is:​
Solution:

There are 12 even numbers between 1 to 25
Consider the given events.
A = Even number ticket in the first draw
B = Even number ticket in the second draw
Now, P(A) = 12/25
P(B/A) = 11/24
Required probability : P(A⋂B) = P(A) * P(B/A) 
= (12/25) * (11/24)
= 11/50

Recommended Content

Recommended Tests

Related tests
Follow Us
© EduRev