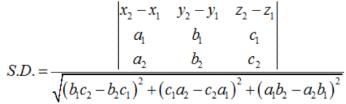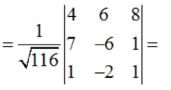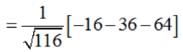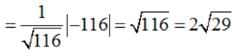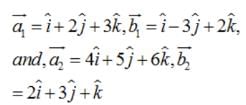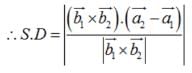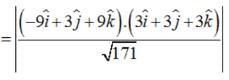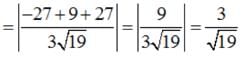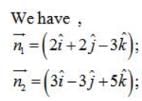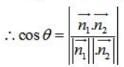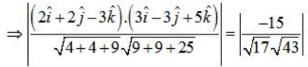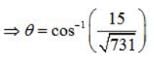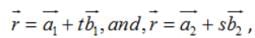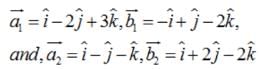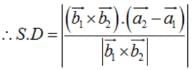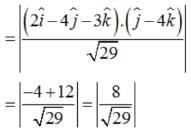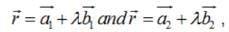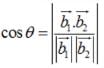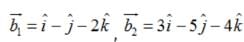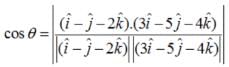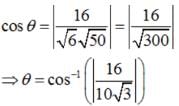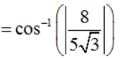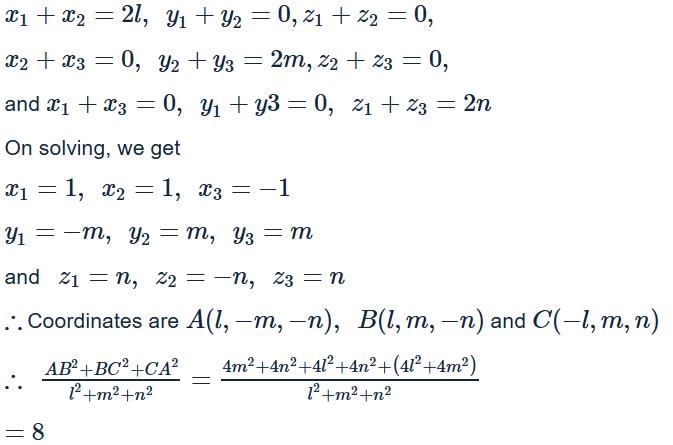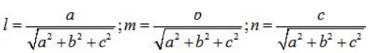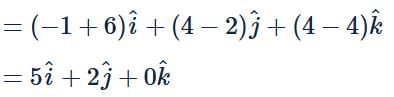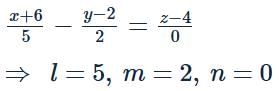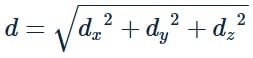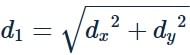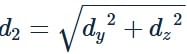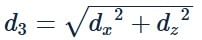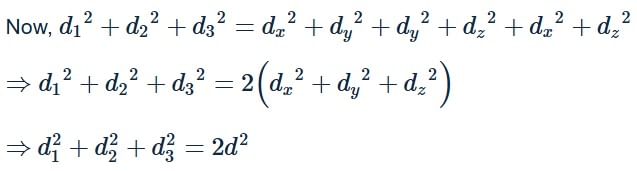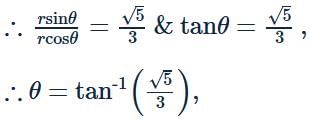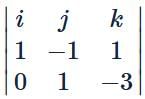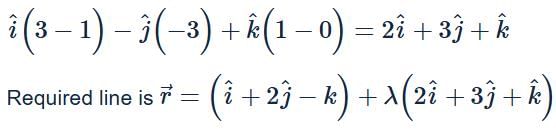Test: Three Dimensional Geometry- 1 - JEE MCQ
25 Questions MCQ Test - Test: Three Dimensional Geometry- 1
The angle θ between the planes A1x + B1y + C1z + D1 = 0 and A2 x + B2 y + C2 z + D2 = 0 is given by
Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.
Find the shortest distance between the lines :
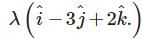
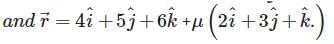
The distance of a point whose position vector is from the plane
Find the angle between the planes whose vector equations are
is a vector joining two points P(x1, y1, z1) and Q(x2, y2, z2). If
Direction cosines of
are
Find the shortest distance between the lines 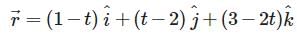 and
and 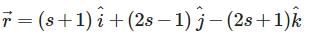
Determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.7x + 5y + 6z + 30 = 0 and 3x – y – 10z + 4 = 0
Find the angle between the following pairs of lines:
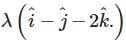 and
and 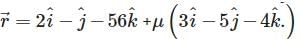
In the following case, determine whether the given planes are parallel orperpendicular, and in case they are neither, find the angles between them. 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
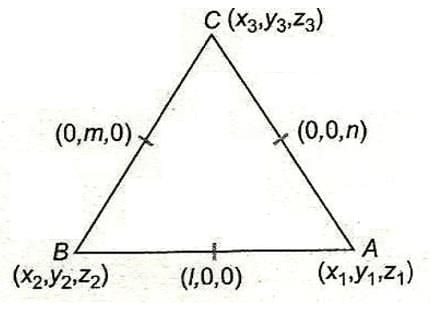
In ∆ABC the mid points of the sides AB, BC and CA repectively (l, 0, 0),(0, m, 0) and (0, 0, n) . Then,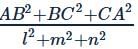 is equal to
is equal to
If l, m, n are the direction cosines and a, b, c are the direction ratios of a line then
The perpendicular bisector of a line segment with end points (1,2,6) and (−3,6,2) passes through (−6,2,4) and has the equation of the form 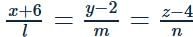 (Where l,m,n are integers, l is a prime number and l>0), then the value of lmn−(l+m+n) equals to
(Where l,m,n are integers, l is a prime number and l>0), then the value of lmn−(l+m+n) equals to
If a line makes angles 90∘, 135∘, 45∘ with the x, y and z – axes respectively, find its direction cosines.
The distance between two points P and Q is d and the length of the projections of PQ on the co-ordinate planes are d1, d2, d3. Then d21+d22 + d23 = kd2 where ‘k’ is
In the vector form, equation of a plane which is at a distance d from the origin, and is the unit vector normal to the plane through the origin is
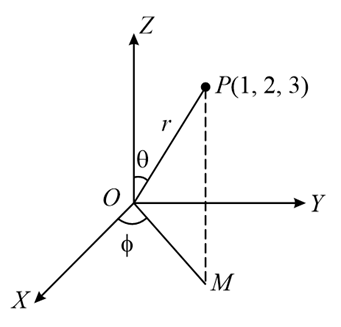
Let PM be the perpendicular from the point P(1, 2, 3) to the XY plane. If OP makes an angle θ with the positive direction of the Z−axis and OM makes an angle ϕ with the positive direction of the X−axis, where O is the origin, then
Determine the direction cosines of the normal to the plane and the distance from the origin. Plane x + y + z = 1
The equation of line through (1,2,−1) and perpendicular to the lines 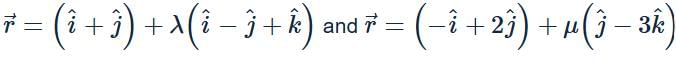 is
is
In the following case, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them. 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0
Let ABC DA′B′C′D′ be a cuboid as shown in the following figure
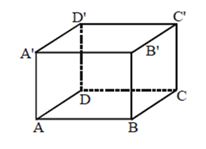
There are twelve face diagonals two on each face. (such as AC and BD, A′C′ and B′D′, etc) How many pairs of them are skew lines (line segments)?