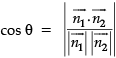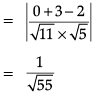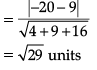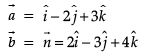All Courses
Get the App Signup / Login
Sign in Open App
JEE Exam  >  JEE Tests  >  Mathematics (Maths) Class 12  >  Test: Three Dimensional Geometry- Case Based Type Questions- 2 - JEE MCQ

Test: Three Dimensional Geometry- Case Based Type Questions- 2 - JEE MCQ


Test Description

15 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Three Dimensional Geometry- Case Based Type Questions- 2

Test: Three Dimensional Geometry- Case Based Type Questions- 2 for JEE 2024 is part of Mathematics (Maths) Class 12 preparation. The Test: Three Dimensional Geometry- Case Based Type Questions- 2 questions and answers have been prepared according to the JEE exam syllabus.The Test: Three Dimensional Geometry- Case Based Type Questions- 2 MCQs are made for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Three Dimensional Geometry- Case Based Type Questions- 2 below.
Solutions of Test: Three Dimensional Geometry- Case Based Type Questions- 2 questions in English are available as part of our Mathematics (Maths) Class 12 for JEE & Test: Three Dimensional Geometry- Case Based Type Questions- 2 solutions in Hindi for Mathematics (Maths) Class 12 course. Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt Test: Three Dimensional Geometry- Case Based Type Questions- 2 | 15 questions in 40 minutes | Mock test for JEE preparation | Free important questions MCQ to study Mathematics (Maths) Class 12 for JEE Exam | Download free PDF with solutions
Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 1
Save

Direction: Read the following text and answer the following questions on the basis of the same:

P1 : x + 3y – z = 0 and P2 : y + 2z = 0 are two intersecting planes. P3 is a plane passing through the point (2, 1, –1) and through the line of intersection of P1 and P2.

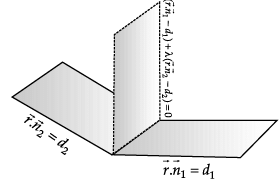
Q. ______ is a point on P3.

Detailed Solution for Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 1
The equation of P3 is x + 9y + 11z = 0.

∴ (–6, –3, 3) is a point on P3.

Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 2
Save

Direction: Read the following text and answer the following questions on the basis of the same:

P1 : x + 3y – z = 0 and P2 : y + 2z = 0 are two intersecting planes. P3 is a plane passing through the point (2, 1, –1) and through the line of intersection of P1 and P2.

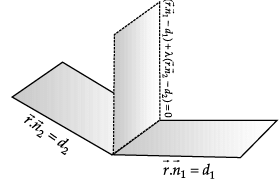
Q. Equation of P3 is _______.

Detailed Solution for Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 2
Let the equation of P3 be P1 + λP2 = 0

i.e., (x + 3y – z) + λ(y + 2z) = 0

P3 passes through the point (2, 1, –1)

∴ (2 + 3 + 1) + λ(1 – 2) = 0

⇒ λ = 6

∴ The equation of P3 is x + 9y + 11z = 0

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 3
Save

Direction: Read the following text and answer the following questions on the basis of the same:

P1 : x + 3y – z = 0 and P2 : y + 2z = 0 are two intersecting planes. P3 is a plane passing through the point (2, 1, –1) and through the line of intersection of P1 and P2.

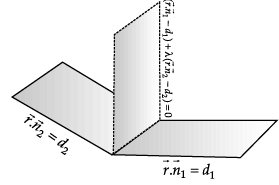
Q. The angle between P1 and P2 is _______.

Detailed Solution for Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 3
M

Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 4
Save

Direction: Read the following text and answer the following questions on the basis of the same:

P1 : x + 3y – z = 0 and P2 : y + 2z = 0 are two intersecting planes. P3 is a plane passing through the point (2, 1, –1) and through the line of intersection of P1 and P2.

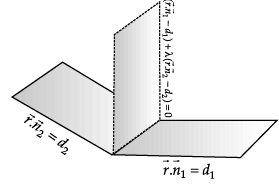
Q. Equation of plane parallel to P3 and passing through (1, 2, 3) is _______.
Detailed Solution for Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 4
The required equation is (x – 1) +9(y – 2) + 11(z – 3) = 0

i.e., x + 9y + 11z – 52 = 0

Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 5
Save

Direction: Read the following text and answer the following questions on the basis of the same:

P1 : x + 3y – z = 0 and P2 : y + 2z = 0 are two intersecting planes. P3 is a plane passing through the point (2, 1, –1) and through the line of intersection of P1 and P2.

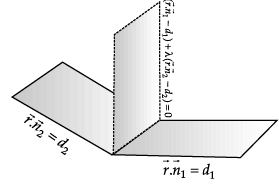
Q. Distance of P3 from origin is _______ units.
Detailed Solution for Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 5
(0, 0, 0) is a point on P3.

∴ Distance of P3 from origin = 0

Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 6
Save

Direction: Read the following text and answer the following questions on the basis of the same:

A mobile tower stands at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with 3 cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at the point (2, 3, 1) as shown in the figure.

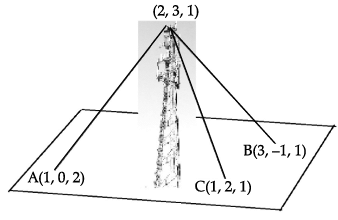
Q. The coordinates of the foot of the perpendicular drawn from the top of the tower to the ground are
Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 7
Save

Direction: Read the following text and answer the following questions on the basis of the same:

A mobile tower stands at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with 3 cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at the point (2, 3, 1) as shown in the figure.

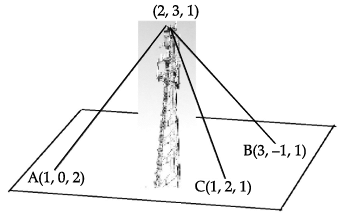
Q. The height of the tower from the ground is
Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 8
Save

Direction: Read the following text and answer the following questions on the basis of the same:

A mobile tower stands at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with 3 cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at the point (2, 3, 1) as shown in the figure.

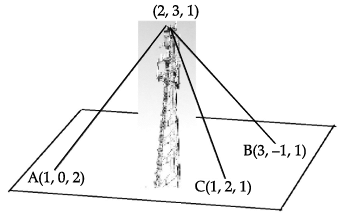
Q. The equation of the plane passing through the points A, B and C is
Detailed Solution for Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 8
A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1)

(x - 1)(1 + 2) -y (-2, 0) + (z - 2) (4 - 0)

3x - 3 + 2y + 4z - 8 = 0

3x + 2y + 4z = 11

Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 9
Save

Direction: Read the following text and answer the following questions on the basis of the same:

A mobile tower stands at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with 3 cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at the point (2, 3, 1) as shown in the figure.

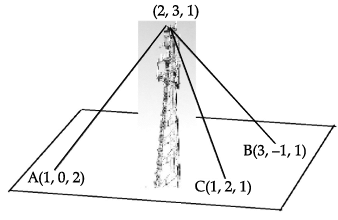
Q. The equation of the perpendicular line drawn from the top of the tower to the ground is
Detailed Solution for Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 9
a = 3, b = 2, c = 4 and

(x1, y1, z1) ≡ (2, 3, 1)

∴ (x-2)/3 = (y-3)/2

= (z-1)/4

Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 10
Save

Direction: Read the following text and answer the following questions on the basis of the same:

A mobile tower stands at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with 3 cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at the point (2, 3, 1) as shown in the figure.

Q. The area of ΔABC is
Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 11
Save

Direction: Read the following text and answer the following questions on the basis of the same:

Consider the plane π1 : 2x – 3y + 4z + 9 = 0 and the point P(1, –2, 3). π1 is a plane parallel to π1 and containing the point P.

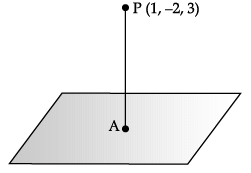
Q. The co-ordinates of A are _______.
Detailed Solution for Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 11
Generally A = (2λ + 1, –3λ – 2, 4λ + 3).

A is a point on π1.

⇒ 2(2λ +1) –3 (–3λ – 2) + 4 (4λ + 3) + 9 = 0

⇒ 29λ + 29 = 0

⇒ λ = –1

∴ A = (–1, 1, –1)

Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 12
Save

Direction: Read the following text and answer the following questions on the basis of the same:

Consider the plane π1 : 2x – 3y + 4z + 9 = 0 and the point P(1, –2, 3). π1 is a plane parallel to π1 and containing the point P.

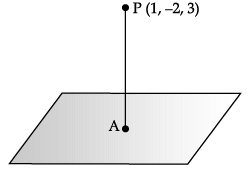
Q. Distance between π1 and π2 is _______ units.
Detailed Solution for Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 12
Distance between π1 and π2

Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 13
Save

Direction: Read the following text and answer the following questions on the basis of the same:

Consider the plane π1 : 2x – 3y + 4z + 9 = 0 and the point P(1, –2, 3). π1 is a plane parallel to π1 and containing the point P.

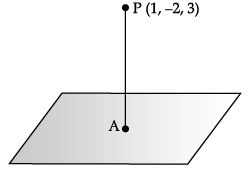
Q. Equation of π2 is _______.
Detailed Solution for Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 13
Equation of π2 is 2(x – 1) –3(y + 2) +4(z – 3) = 0

i.e., 2x – 3y + 4z – 20 = 0

Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 14
Save

Direction: Read the following text and answer the following questions on the basis of the same:

Consider the plane π1 : 2x – 3y + 4z + 9 = 0 and the point P(1, –2, 3). π1 is a plane parallel to π1 and containing the point P.

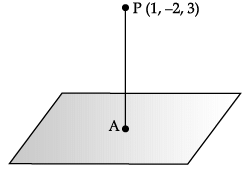
Q. A is the foot of perpendicular from π to π1. Equation of PA is _______.
Detailed Solution for Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 14
Here

Equation of PA is

Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 15
Save

Direction: Read the following text and answer the following questions on the basis of the same:

Consider the plane π1 : 2x – 3y + 4z + 9 = 0 and the point P(1, –2, 3). π1 is a plane parallel to π1 and containing the point P.

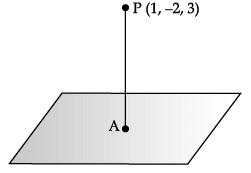
Q. The image of π on π1 is _______.
Detailed Solution for Test: Three Dimensional Geometry- Case Based Type Questions- 2 - Question 15
Let P′(α, β, γ) be the image A is mid-point of PP′.

⇒ α = –3, β = 4, γ = –5

∴ P′ = (–3, 4, –5)

204 videos|290 docs|139 tests
Join Course
Information about Test: Three Dimensional Geometry- Case Based Type Questions- 2 Page
In this test you can find the Exam questions for Test: Three Dimensional Geometry- Case Based Type Questions- 2 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Three Dimensional Geometry- Case Based Type Questions- 2, EduRev gives you an ample number of Online tests for practice

Top Courses for JEE

204 videos|290 docs|139 tests
Join Course
Download as PDF

Top Courses for JEE

Important Questions for Three Dimensional Geometry- Case Based Type Questions- 2

Find all the important questions for Three Dimensional Geometry- Case Based Type Questions- 2 at EduRev.Get fully prepared for Three Dimensional Geometry- Case Based Type Questions- 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Three Dimensional Geometry- Case Based Type Questions- 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Three Dimensional Geometry- Case Based Type Questions- 2 resources.

Three Dimensional Geometry- Case Based Type Questions- 2 MCQs with Answers

Prepare for the Three Dimensional Geometry- Case Based Type Questions- 2 within the JEE exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Three Dimensional Geometry- Case Based Type Questions- 2 Mathematics (Maths) Class 12

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Three Dimensional Geometry- Case Based Type Questions- 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup