Test: Application of Integrals- Assertion & Reason Type Questions - Commerce MCQ
6 Questions MCQ Test - Test: Application of Integrals- Assertion & Reason Type Questions
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): If the two curves y = f(x) and y = g(x) intersect at x = a, x = c and x = b, such that a < c="" />< />
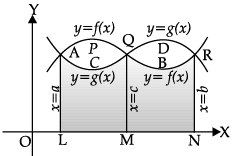
If f(x) > g(x) in [a, c] and g(x) £ f(x) in [c, b], then Area of the regions bounded by the curve
= Area of region PACQP + Area of region QDRBQ.
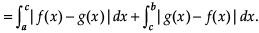
Reason (R): Let the two curves by y = f(x) and y = g(x), as shown in the figure. Suppose these curves intersect at f(x) with width dx.
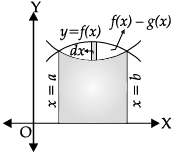
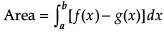
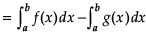
= Area bounded by the curve {y = f(x)}
–Area bounded by the curve {y = g(x)}, where f(x) > g(x).


Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): The area enclosed by the circle x2 + y2 = a2 is πa2.
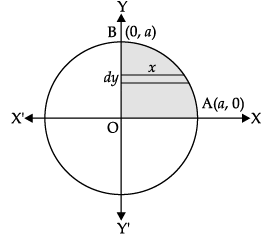
Reason (R): The area enclosed by the circle
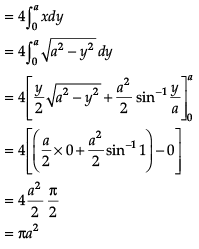

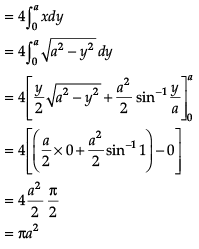
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): The area enclosed by the circle x2 + y2 = a2 is πa2.
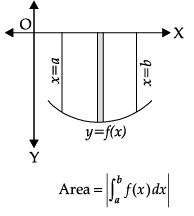
Reason (R): If the curve under consideration lies below x-axis, then f(x) < 0 from x = a to x = b, the area bounded by the curve y = f(x) and the ordinates x = a, x = b and x-axis is negative. But, if the numerical value of the area is to be taken into consideration, then
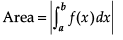

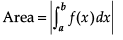
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): The area of the region bounded by the curve y = x2 and the line y = 4 is 3/32.
Reason (R):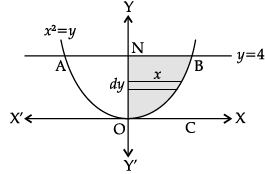
Since the given curve represented by the equation y = x2 is a parabola symmetrical about y-axis only, therefore, from figure, the required area of the region AOBA is given by
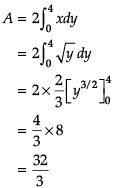
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A):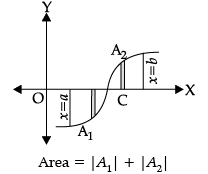
Reason (R): It may happen that some portion of the curve is above x-axis and some portion is below x-axis as shown in the figure. Let A1 be the area below the x-axis and A2 be the area above the x-axis. Therefore, area bounded by the curve y = f(x), x-axis and the ordinates x = a and x = b is given by Area = |A1| + |A2|
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A):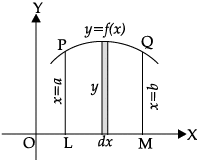 The area of region PQML
The area of region PQML
![]()
Reason (R):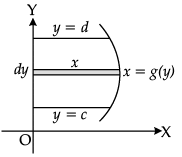 The area A of the region bounded by curve x = g(y), y-axis and the lines y = c and y = d is given by
The area A of the region bounded by curve x = g(y), y-axis and the lines y = c and y = d is given by
![]()














