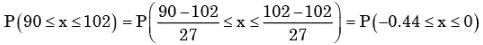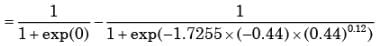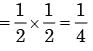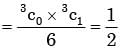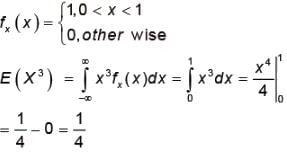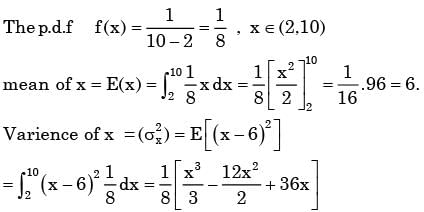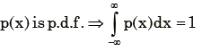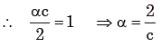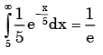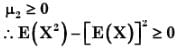Test: Statistics Part:- 1 - Mathematics MCQ
20 Questions MCQ Test - Test: Statistics Part:- 1
The standard normal probability function can be approximated as
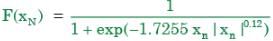
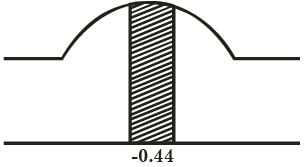
Where xN = standard normal deviate. If mean and standard deviation of annual precipitation are 102 cm and 27 cm respectively, the probability that the annual precipitation will be between 90 and 102 cm is
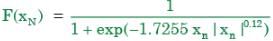
Where xN = standard normal deviate. If mean and standard deviation of annual precipitation are 102 cm and 27 cm respectively, the probability that the annual precipitation will be between 90 and 102 cm is
Two coins are simultaneously tossed. The probability of two heads simultaneously appearing is
There are two containers, with one containing 4 Red and 3 Green balls and the other containing Blue and 4 Green balls. One bal is drawn at random form each container. The probability that one of the ball is Red and the other is Blue will be
A fair coin is tossed three times in succession. If the first toss produces a head, then the probability of getting exactly two heads in three tosses is
Two fair dice are rolled and the sum r of the numbers turned up is considered
A box contains 4 white balls and 3 red balls. In succession, two balls are randomly selected and removed from the box. Given that the first removed ball is white, the probability that the second removed ball is red is
X is a uniformly distributed random variable that takes values between 0 and 1. The value of E{X3} will be
Consider a Gaussian distributed random variable with zero mean and standard deviation σ. The value of its cumulative distribution function at the origin will be
A random variable is uniformly distributed over the interval 2 to 10. Its variance will be
The probability that there are 53 Sundays in a randomly chosen leap year is
You have gone to a cyber-café with a friend. You found that the cyber-cafe has only three terminals. All terminals are unoccupied. You and your friend have to make a random choice of selecting a terminal. What is the probability that both of you will NOT select the same terminal?
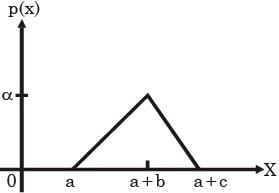
Probability density function p(x) of a random variable x is as shown below. The value of α is
Two dices are rolled simultaneously. The probability that the sum of digits on the top surface of the two dices is even, is
Poisson's ratio for a metal is 0.35. Neglecting piezo-resistance effect, the gage factor of a strain gage made of this metal is
Assume that the duration in minutes of a telephone conversation follows the exponential distribution 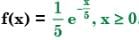 The probability that the conversation will exceed five minutes is
The probability that the conversation will exceed five minutes is
Using the given data points tabulated below, a straight line passing through the origin is fitted using least squares method. The slope os the line is

The function y = sin φ, (φ > 0) is approximated as y = φ, where φ is in radian. The maximum value of φ for which the error due to the approximation is with in 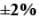 is
is
If two fair coins are flipped and at least one of the outcome is know to be a head, what is the probability that both outcomes are heads?
If the difference between the expectation of the square of a random variable ( E [X])2 is denoted by R, then
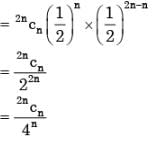
For each element is a set of size 2n, an unbiased coin is tossed. The 2n coin tossed are independent. An element is chosen if the corresponding coin toss were head. The probability that exactly n elements are chosen is