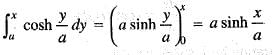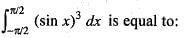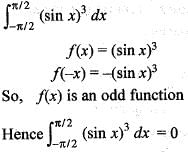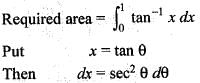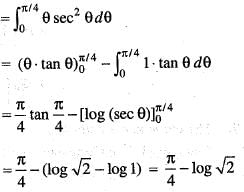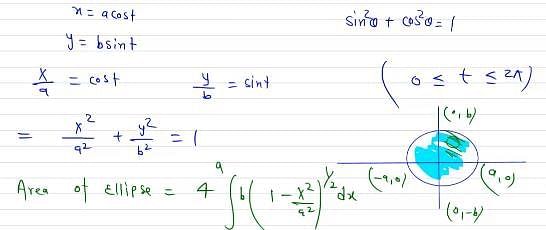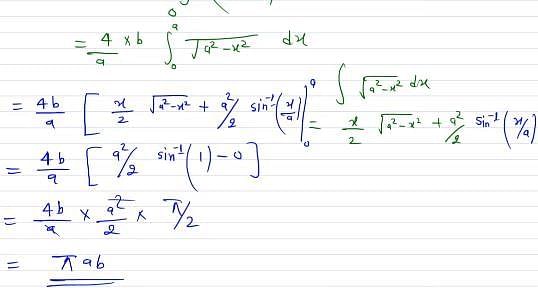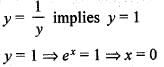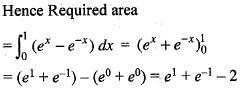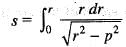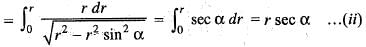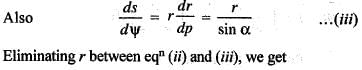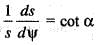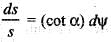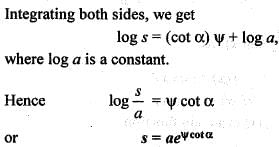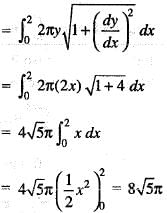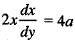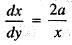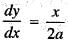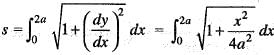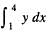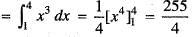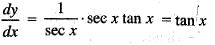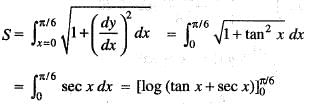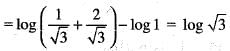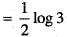Integral Calculus -3 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Integral Calculus -3
The moment of inertia of a hollow sphere about a diameter is:
The area bounded by the curve  from x = 0 to x = 1, the x -axis and the ordinate at x = 1 is:
from x = 0 to x = 1, the x -axis and the ordinate at x = 1 is:
The area of the closed curve x = a cos t, y = b sint is given by:
The area bounded by the curves y = ex, y = e-x and the line x = 1, is:
The intrinsic equation of the curve p = r sin α is given by:
The area of surface of the solid generated by the revolution of the line segment y = 2x from x = 0 to x = 2, about x-axis is equal to:
The length of the arc of the parabola x2 = 4ay from the vertex to the extremity of the latus rectum is given by:
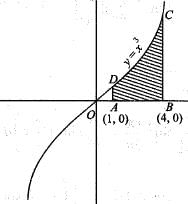
The area bounded by the curve y = x3, x -axis and the line x = 1 and x = 4 is given by:
The length of the arc of the curve y = log sec x between x = 0 and x = π/6 is equal to:
|
27 docs|150 tests
|


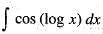 equals:
equals: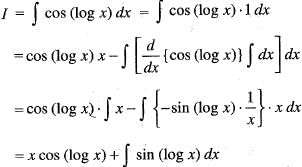
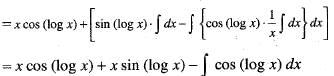
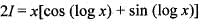
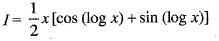
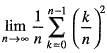 is equal to:
is equal to: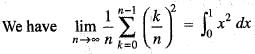
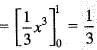

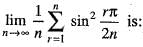
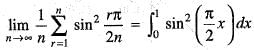
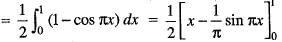
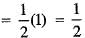
 is equal to:
is equal to: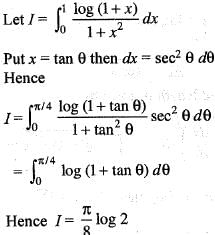
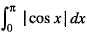 is equal to:
is equal to: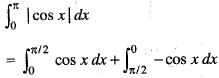
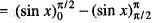
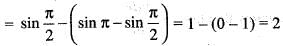
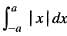 is equal to:
is equal to: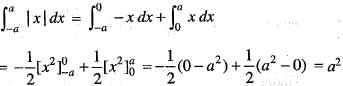
 sin2 ucos2 udu, then:
sin2 ucos2 udu, then: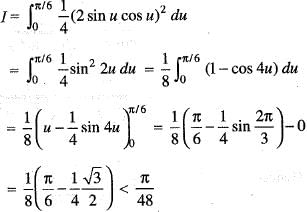
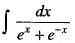 is equal to:
is equal to: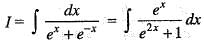
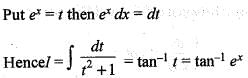
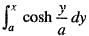 is equal to:
is equal to: