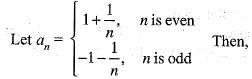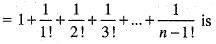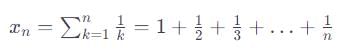Sequences And Series Of Real Numbers -10 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Sequences And Series Of Real Numbers -10
What is the set of all the distinct elements of a sequence called?
The limit superior and limit inferior of 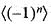 is respectively given by
is respectively given by
Let ∑an be a convergent series of positive terms and let ∑bn be a divergent series of positive terms. Then,
Consider the alternating series 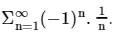 . What is true about the convergence of this series?
. What is true about the convergence of this series?
A: Sequence 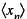 is convergent.
is convergent.
B: Sequence 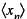 is bounded.
is bounded.
Let the sequence be 1, 3, 5, 7, 9……… then this sequence is ____________
For the sequence {xn}, where xn = 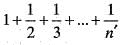 consider the following statements
consider the following statements
I. {xn} is a Cauchy sequence
II. {xn} is not convergent
III. {xn} is not bounded
Select the correct answer using the codes given below
Let f : R → R be a strictly increasing continuous function. If {an} is a sequence in [0, 1], then the sequence {f(an)} is
Which of the following statement is/are correct?
Every Cauchy sequence of reai numbers, is
If a > 1, s1 = 1, sn+1 = Then sequence <sn> is
|
27 docs|150 tests
|