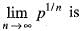Sequences And Series Of Real Numbers -7 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Sequences And Series Of Real Numbers -7
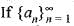 is a sequence of real numbers satisfying
is a sequence of real numbers satisfying 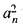
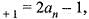 then
then
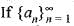 is a sequence of real numbers satisfying
is a sequence of real numbers satisfying 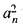
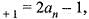 then
thenIf x1 = 4 and 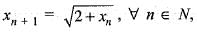 then the sequence {xn} converge to
then the sequence {xn} converge to
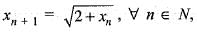 then the sequence {xn} converge to
then the sequence {xn} converge toLet (an) be an increasing sequence of positive real numbers such that the series is divergent. Let
for n = 2, 3, .... Then
tn is equal to
Which of the following series is divergent?
Let ∑un be a series of positive terms such that 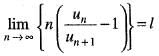 Then,
Then,
(i) if l > 1, the series converges;
(ii) if l < 1, the series diverges;
(iii) if l = 1, the series may either converge or diverge and therefore the test fails;
This theorem is known as
The set of all x at which the power series converges is
If {xn} is a sequence of real numbers, then match list I with list II and select the correct answer using codes given below the lists
List I (sequences)
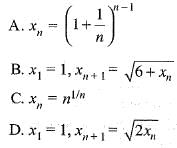
List II (limit of sequences)


∑un is a series of positive terms. If Sn = u1 + n2 + ... + un, then
Which amongst the following expressions is not true?
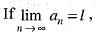 where an > 0
where an > 0  n, then (a1 a2 a3...an)1/n = l. Above theorem is known as
n, then (a1 a2 a3...an)1/n = l. Above theorem is known as
Which amongst the following expresses the Cauchy’s first theorem on limits?
|
27 docs|150 tests
|



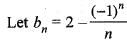 and an = bn - bn + 1 then the series ∑an
and an = bn - bn + 1 then the series ∑an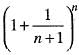 converge to
converge to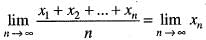 only of
only of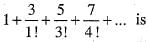
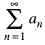 converges, then sequence
converges, then sequence 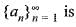
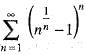
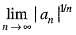 is equal to
is equal to 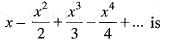
 By I the series is absolutely convergent when x lies between −1 and +1
By I the series is absolutely convergent when x lies between −1 and +1