Vector Calculus - 5 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Vector Calculus - 5
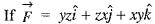 and S is that part of the surface of the sphere x2 + y2 + z2 = 1 which lies in the first octant, then the value of
and S is that part of the surface of the sphere x2 + y2 + z2 = 1 which lies in the first octant, then the value of 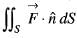 is
is
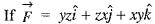 and S is that part of the surface of the sphere x2 + y2 + z2 = 1 which lies in the first octant, then the value of
and S is that part of the surface of the sphere x2 + y2 + z2 = 1 which lies in the first octant, then the value of 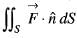 is
is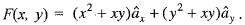 It’s line integral over the straight line from (x, y) = (0, 2) to (x, y) = (2, 0) evaluates to
It’s line integral over the straight line from (x, y) = (0, 2) to (x, y) = (2, 0) evaluates to
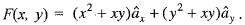 It’s line integral over the straight line from (x, y) = (0, 2) to (x, y) = (2, 0) evaluates to
It’s line integral over the straight line from (x, y) = (0, 2) to (x, y) = (2, 0) evaluates to The line integral of  where, C is the unit circle around the origin traversed once in the counter-clockwise direction, is
where, C is the unit circle around the origin traversed once in the counter-clockwise direction, is
The directional derivative of f(x, y, z) = 2x2 + 3y2 + z2 at the point P(2, 1, 3) in the direction of the vector 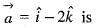
A scalar field is given by f = x2/3 + y2/3, where x and y are the Cartesian coordinates. The derivative of f along the line y = x directed away from the origin, at the point (8, 8) is
Velocity vector of a flow field is given as 
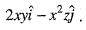 The velocity vector at (1, 1, 1) is
The velocity vector at (1, 1, 1) is
If 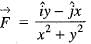 and C is the circle x2 + y2 = 1 traversed counter clockwise, then
and C is the circle x2 + y2 = 1 traversed counter clockwise, then 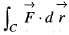 is
is
The value of 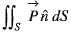 where
where 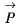 =
= 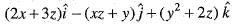 and S is the surface of the sphere having centre at (3, -1, 2) and radius 3 is
and S is the surface of the sphere having centre at (3, -1, 2) and radius 3 is
Equation of the line normal to function fix) = (x - 8)2/3 + 1 at P(0, 5) is
Consider the integral 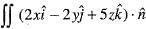 dS over the surface of a sphere of radius -3 with centre at the origin and surface unit normal
dS over the surface of a sphere of radius -3 with centre at the origin and surface unit normal  pointing away from the origin. Using the Gauss’s divergence theorem, the value of this integral is
pointing away from the origin. Using the Gauss’s divergence theorem, the value of this integral is
Consider the points P and Q in the XY-plane, with P = (1, 0) and Q = (0, 1). The line integral  along the sem icircle with the line segment PQ as its diameter
along the sem icircle with the line segment PQ as its diameter
Consider a closed surface S surrounding volume of V. if 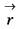 is the position vector o f a point inside S, with
is the position vector o f a point inside S, with  the unit normal on S, the value of the integral
the unit normal on S, the value of the integral 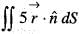 is
is
|
27 docs|150 tests
|




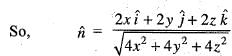
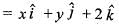
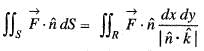 ...(i)
...(i) 
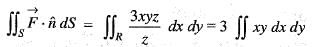

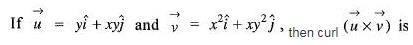



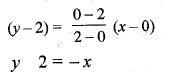
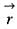 be the position vector in two- dimensional space then,
be the position vector in two- dimensional space then,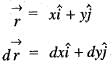
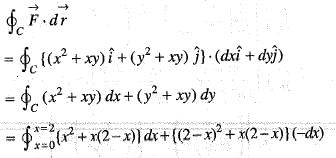
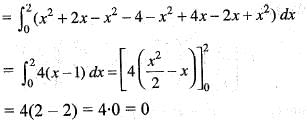
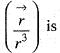

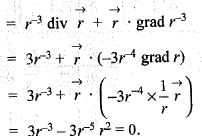
 ....(i)
....(i)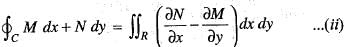
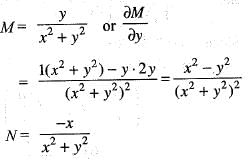
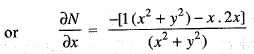
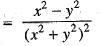
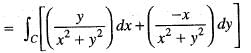
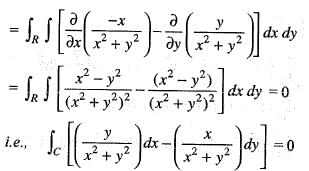
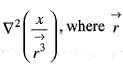 has usual meaning.
has usual meaning.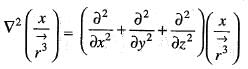
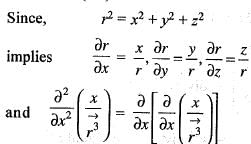
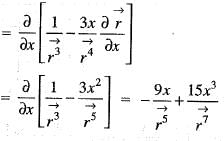
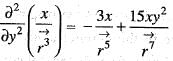
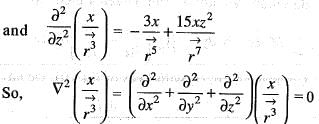
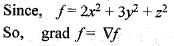

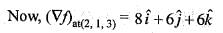
 is nothing but the component of grad f in the direction of vector
is nothing but the component of grad f in the direction of vector 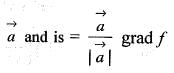
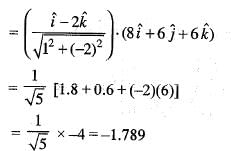
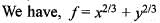
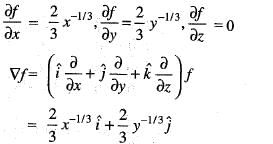
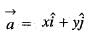 (Putting y = x)
(Putting y = x)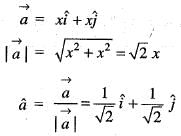
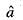

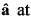 the point (8 , 8)
the point (8 , 8)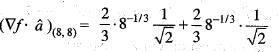
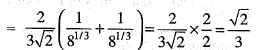
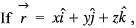 then the value of curl
then the value of curl 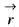 will be
will be
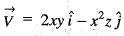

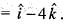


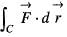
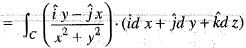
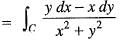
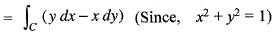 Since, the parametric equation of given circle a
Since, the parametric equation of given circle a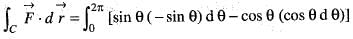
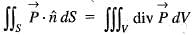
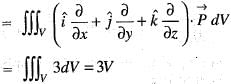
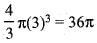
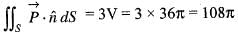
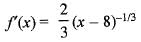
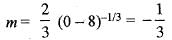
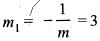
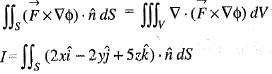
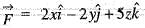
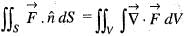

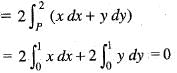
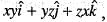 , the div v is
, the div v is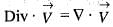

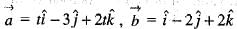 and
and  the value of
the value of 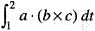 is
is 
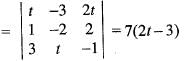
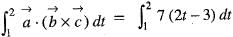


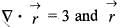 is the position vector)
is the position vector)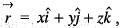 then the value of curl
then the value of curl 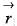 will be
will be
















