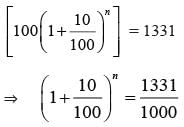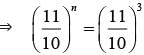Olympiad Test: Compound Interest - Class 7 MCQ
20 Questions MCQ Test Mathematics Olympiad Class 7 - Olympiad Test: Compound Interest
Find compound interest on Rs 7500 at 4% per annum for 2 years, compounded annually.
Find the compound interest on Rs 16,000 at 20% per annum for 9 months, compounded quarterly.
Simple interest on a certain sum of money for 3 years at 8% per annum is half the compound interest on Rs 4000 for 2 years at 10% per annum. The sum placed on simple interest is:
Anil invested an amount of Rs 8000 in a fixed deposit scheme for 2 years at compound interest rate 5% per annum. How much amount will Anil get on maturity of the fixed deposit?
The present worth of Rs 169 due in 2 years at 4% per annum compound interest is:
On a sum of money, the simple interest for 2 years is Rs 660, while the compound interest is Rs 696.30, the rate of interest being the same in both the cases. The rate of interest is:
The difference between simple interest and compound interest on Rs 1200 for one year at 10% per annum reckoned half yearly is
A sum of money invested at compound interest amounts to Rs 800 in 3 years and to Rs 840 in 4 years. The rate of interest per annum is
If the simple interest on a sum of money for 2 years at 5% per annum is Rs 50, what is the compound interest on the same at the same rate and for the same time?
In what time will Rs 1000 become Rs 1331 at 10% per annum compounded annually?
If the simple interest on a sum of money at 5% per annum for 3 years is Rs 1200, find the compound interest on the same sum for the same period at the same rate.
What will be the compound interest on a sum of Rs 25,000 after 3 years at the rate of 12% per annum?
The compound interest on Rs 30,000 at 7% per annum is Rs 4347. The period (in years) is
The difference between compound interest and simple interest on an amount of Rs 15,000 for 2 years is Rs 96. What is the rate of interest per annum?
The compound interest on a certain sum for 2 years at 10% per annum is Rs 525. The simple interest on the same sum for double the time at half the rate percent per annum is:
At what rate of compound interest per annum will a sum of Rs 1200 become Rs 1348.32 in 2 years?
The least number of complete years in which a sum of money invested at 20% compound interest will be more than double is:
The effective annual rate of interest corresponding to a nominal rate of 6% per annum payable half-yearly is:
There is 60% increase in an amount in 6 years at simple interest. What will be the compound interest of Rs 12,000 after 3 years at the same rate?
A bank offers 5% compound interest calculated on half-yearly basis. A customer deposits Rs 1600 each on 1st January and 1st July of a year. At the end of the year, the amount he would have gained by way of interest is:
|
24 videos|57 docs|100 tests
|