Olympiad Test: Elementary Mensuration-II - 2 - Class 7 MCQ
20 Questions MCQ Test Mathematics Olympiad Class 7 - Olympiad Test: Elementary Mensuration-II - 2
What is the capacity of the cylindrical tank?
I. The area of the base is 61,600 sq. cm.
II. The height of the tank is 1.5 times the radius.
III. The circumference of base is 880 cm.
I. The area of the base is 61,600 sq. cm.
II. The height of the tank is 1.5 times the radius.
III. The circumference of base is 880 cm.
Three pipes A, B and C can fill an empty tank fully in 30 minutes, 20 minutes, and 10 minutes respectively. When the tank is empty, all the three pipes are opened. A, B and C discharge chemical solutions P, Q and R respectively. What is the proportion of the solution R in the liquid in the tank after 3 minutes?
Pipes A and B can fill a tank in 5 and 6 hours respectively. Pipe C can empty it in 12 hours. If all the three pipes are opened together, then the tank will be filled in
A pump can fill a tank with water in 2 hours. Because of a leak, it took 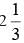 hours to fill the tank. The leak can drain all the water of the tank in:
hours to fill the tank. The leak can drain all the water of the tank in:
Two pipes A and B can fill a cistern in 37.5 minutes and 45 minutes respectively. Both pipes are opened. The cistern will be filled in just half an hour, if B is turned off after:
A tank is filled by three pipes with uniform flow. The first two pipes operating simultaneously fill the tank in the same time during which the tank is filled by the third pipe alone. The second pipe fills the tank 5 hours faster than the first pipe and 4 hours slower than the third pipe. The time required by the first pipe is:
Two pipes can fill a tank in 20 and 24 minutes respectively and a waste pipe can empty 3 gallons per minute. All the three pipes working together can fill the tank in 15 minutes. The capacity of the tank is:
A tank is filled in 5 hours by three pipes A, B and C. The pipe C is twice as fast as B and B is twice as fast as A. How much time will pipe A alone take to fill the tank?
Two pipes A and B together can fill a cistern in 4 hours. Had they been opened separately, then B would have taken 6 hours more than A to fill the cistern. How much time will be taken by A to fill the cistern separately?
Two pipes A and B can fill a tank in 20 and 30 minutes respectively. If both the pipes are used together, then how long will it take to fill the tank?
Two pipes A and B can fill a tank in 15 minutes and 20 minutes respectively. Both the pipes are opened together but after 4 minutes, pipe A is turned off. What is the total time required to fill the tank?
One pipe can fill a tank three times as fast as another pipe. If together the two pipes can fill the tank in 36 minutes, then the slower pipe alone will be able to fill the tank in:
A large tanker can be filled by two pipes A and B in 60 minutes and 40 minutes respectively. How many minutes will it take to fill the tanker from empty state if B is used for half the time and A and B fill it together for the other half?
A tap can fill a tank in 6 hours. After half the tank is filled, three more similar taps are opened. What is the total time taken to fill the tank completely?
Three taps A, B and C can fill a tank in 12, 15 and 20 hours respectively. If A is open all the time and B and C are open for one hour each alternately, the tank will be full in:
Three pipes A, B and C can fill a tank in 6 hours. After working at it together for 2 hours, C is closed and A and B can fill the remaining part in 7 hours. The number of hours taken by C alone to fill the tank is:
How much time will the leak take to empty the full cistern?
I. The cistern is normally filled in 9 hours.
II. It takes one hour more than the usual time to fill the cistern because of a leak in the bottom.
How long will it take to empty the tank if both the inlet pipe A and the outlet pipe B are opened simultaneously?
I. A can fill the tank in 16 minutes.
II. B can empty the full tank in 8 minutes.
If both the pipes are opened, how many hours will be taken to fill the tank?
I. The capacity of the tank is 400 litres.
II. The pipe A fills the tank in 4 hours.
III. The pipe B fills the tank in 6 hours.
Find the number of lead balls of diameter 1 cm each that can be made from a sphere of diameter 16 m.
|
24 videos|57 docs|100 tests
|



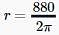

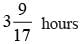
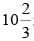 min
min
















